Skip to main content Link Search Menu Expand Document (external link)
logo img  50.002 CS

50.002 Computation Structures
Information Systems Technology and Design
Singapore University of Technology and Design

State Machine

Each topic’s questions are grouped into three categories: basic, intermediate, and challenging. You are recommended to do all basic problem set before advancing further.

Classifying FSM (Basic)

The diagram below illustrates the FSM diagram of a machine that has the same purpose. The circle that is bolded signifies the starting state.

State whether the following is true or false and explain your answer:

  • Statement 1: “Diagram A illustrates a Mealy machine.”
  • Statement 2: “Diagram B can be further minimized.”

What is the purpose of these FSMs?

Show Answer

Statement 1 is false because the machine in Diagram A has its output that depends only on its state. Statement 2 is **true**, we can minimise it into just two states because S1 and S2 are equivalent.

The purpose of both machines is to detect the presence of an edge and output a 1 once for the cycle where the edge happens, and 0 otherwise.


Your friend plot the timing diagram of the machine in Diagram A and obtain the following output:

Assume that the machine starts at S0. While referring to the FSM diagram up above, write the current state that occurs at instances [A], [B], [C], and [D] respectively.

Show Answer

We can obtain the answers easily by running the FSM step by step. At each labeled instance, the machine is at the following states:

  • [A]: S0,
  • [B]: S2,
  • [C]: S1,
  • [D]: S0,

An Incomplete State Machine (Basic)

The ACME Company has recently received an order from a Mr. Wiley E. Coyote for their all-digital Perfectly Perplexing Padlock:

  • The P3 has two buttons (“0” and “1”) that when pressed cause the FSM controlling the lock to advance to a new state.
  • In addition to advancing the FSM, each button press is encoded on the B signal (B=0 for button “0”, B=1 for button “1”).
  • The padlock unlocks when the FSM sets the UNLOCK output signal to 1, which it does whenever the last N button presses correspond to the unique N-digit combination.

Unfortunately the design notes for the P3 are incomplete. Using the specification above and clues gleaned from the partially completed diagrams below fill in the information that is missing from the state transition diagram with its accompanying truth table.

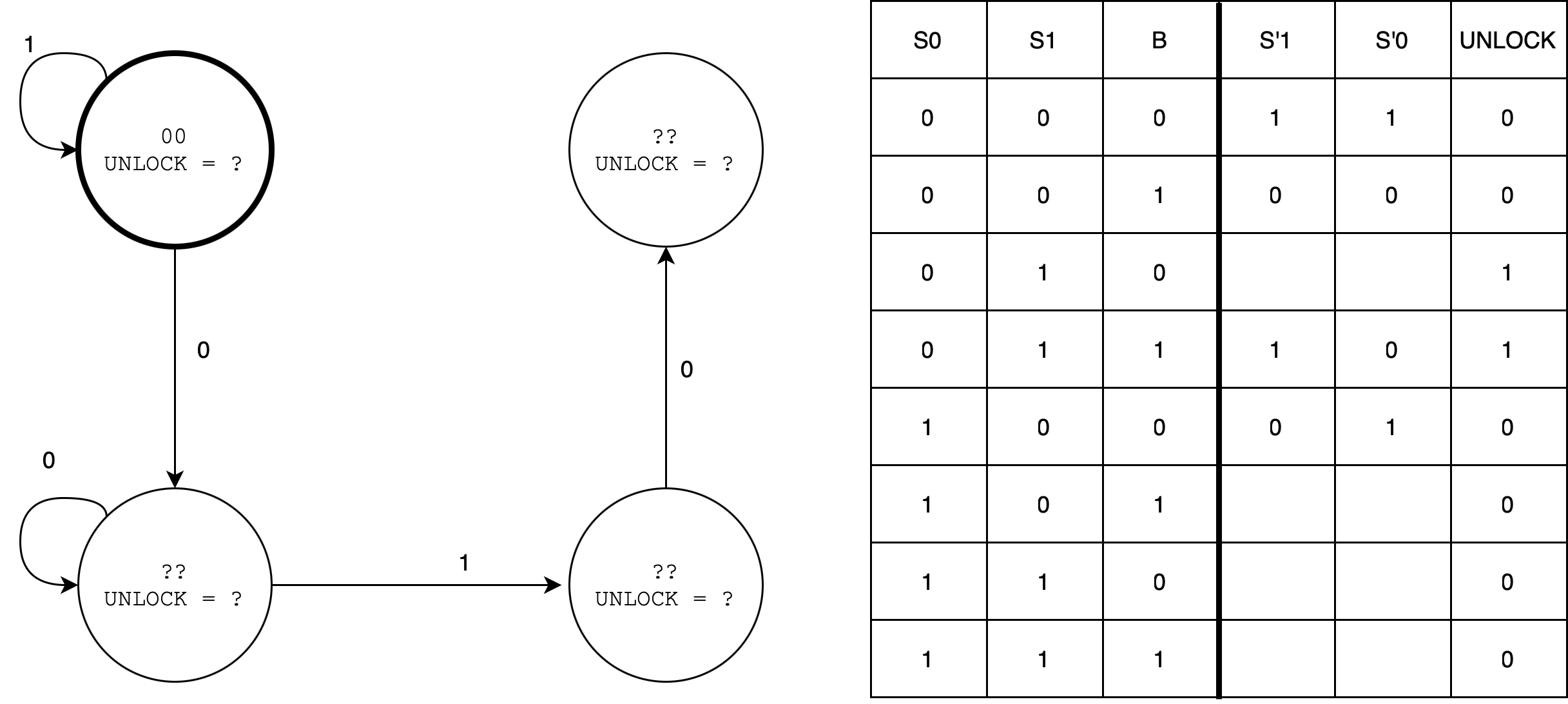
When done,

  • Each state in the transition diagram should be assigned a 2-bit state name S1S0 (note that in this design the state name is not derived from the combination that opens the lock),
  • The arcs leaving each state should be mutually exclusive and collectively exhaustive,
  • The value for UNLOCK should be specified for each state, and the truth table should be completed.

Also, what is the combination of the lock?

Show Answer

This state machine is a Moore machine. The completed state transition diagram and truth table is as follows:

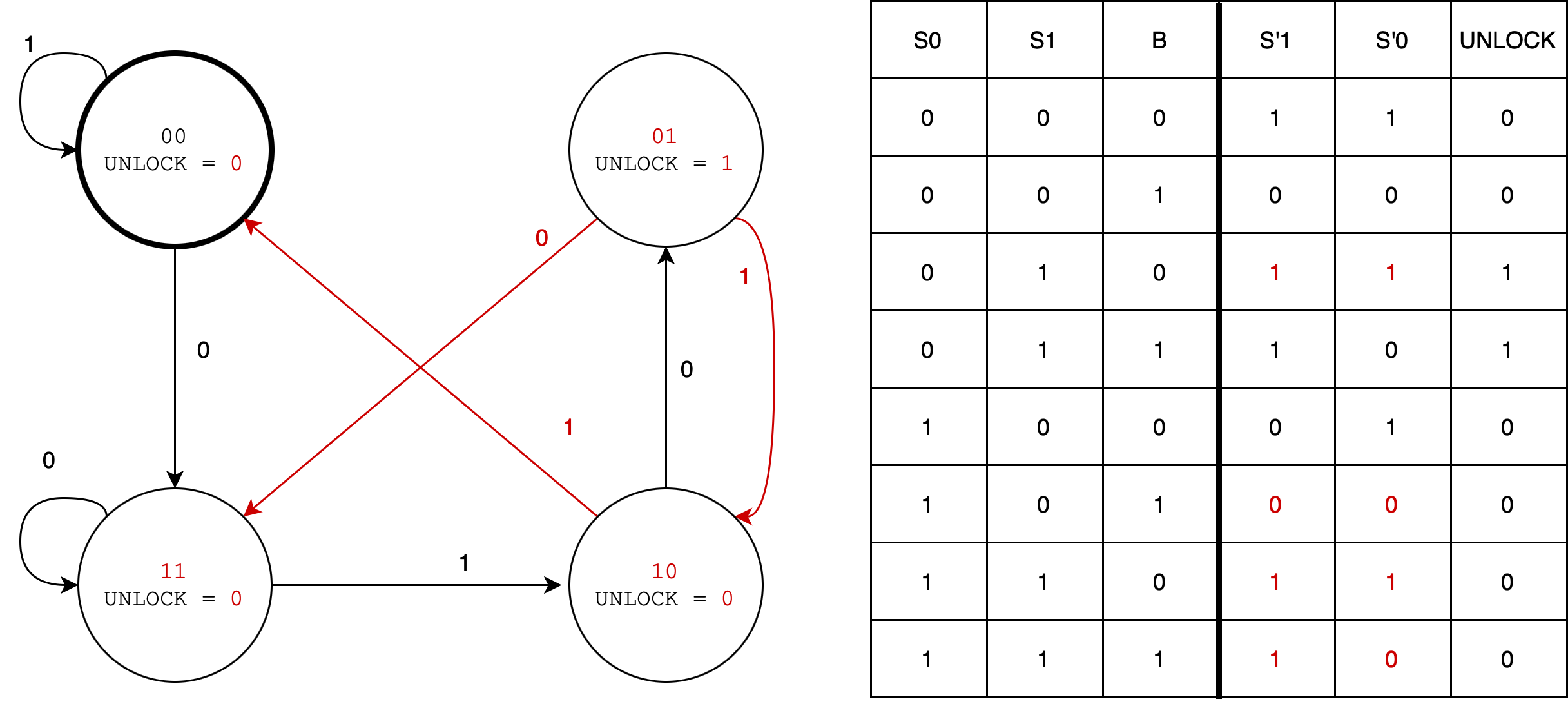
The combination for the lock is 100.

Constructing an FSM (Basic)

Construct a divisible-by-3 Moore FSM that accepts a binary number entered one bit at a time. The most significant bit entered first, and the FSM should indicate with an output light (1 bit) if the number entered so far is divisible by 3.

Hint

The FSM has 3 states.

Answer the following questions:

  1. Draw a state transition diagram for your FSM indicating the initial state and for which states the light should be turned on.
    Show Answer

    If the **value** of the number entered so far is `N`, then if digit `b` is entered next, the value of the new number `N'` is `2N + b`. Using this fact:

    • If `N mod 3 == 0` then for some integer `p`,` N = 3p + 0`. After the digit b is entered, `N' = 6p + b`. So `N'` is `b mod 3`.
    • If `N mod 3 == 1` then for some integer `p`, `N = 3p + 1`. After the digit b is entered, `N' = 6p + 2 + b`. So `N'` is `b+2 mod 3`.
    • If `N mod 3 == 2` then for some integer `p`, `N = 3p + 2`. After the digit b is entered, `N' = 6p + 4 + b`. So `N'` is `b+1 mod 3`.

    This leads to the following transition diagram where each state corresponds to each of the possible values of `N mod 3`.

  2. Construct a truth table for the FSM logic. Inputs include the state bits and the next bit of the number; outputs include the next state bits and the control for the light. Remember that this should be a Moore machine, so the output (light) should follow the current state output and not the next state.
    Show Answer

    $$ \begin{matrix} S_1 & S_0 & b & S_1' & S_0' & \text{light} \\ \hline 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 \\ \hline \end{matrix} $$


  3. Write down the boolean equation for the FSM.
    Show Answer

    The boolean equation for the FSM is: $$ \begin{aligned} \text{light } &= \overline{S_1} \cdot \overline{S_0}\\ S_1' &= \overline{S_1} \cdot S_0 \cdot \overline{b} + S_1 \cdot \overline{S_0} \cdot b \\ S_0' &= \overline{S_1} \cdot \overline{S_0} \cdot b + S_1 \cdot \overline{S_0} \cdot \overline{b}\\ \end{aligned} $$


Hardware Implementation of a state machine (Intermediate)

Consider the schematic of a machine as follows, which function is to: detect a sequence of three or more consecutive 1’s, and output: 1 after three or more consecutive 1’s, or 0 otherwise.

Video explanation here.

Let’s analyse the circuit by answering the questions below:

  1. If the circuit has an initial state of AB=00, and the input at t=0 is x=0, what will the immediate next state be?
    Show Answer

    The immediate next state is: AB = 00. You can easily trace this output from the circuit above.


  2. If the circuit has an initial state of AB=00, and the input at t=0 is x=1, what will the immediate next state be?
    Show Answer

    The immediate next state is: AB = 01. You can easily trace this output from the circuit above.


  3. If the circuit has a current state AB=01, and the current input is x=1, what will the immediate next state be?
    Show Answer

    The immediate next state is: AB = 10. You can easily trace this output from the circuit above.


  4. If the circuit has a current state AB=11, and the current input is x=1, what will the immediate next state be?
    Show Answer

    The immediate next state is: AB = 11. You can easily trace this output from the circuit above.


  5. If the circuit has a current state AB=11, and the current input is x=0, what will the immediate next state be?
    Show Answer

    The immediate next state is: AB = 00. You can easily trace this output from the circuit above.


  6. What are the state(s) that can go to state AB=00 as its next state?

    Show Answer

    All combinations: AB=00, 01, 10, or 11. You can prove it easily by brute force: checking if AB = 00 next if its previously set to some value AB = ij given existing value x.


  7. What is the value of output y when the current state is AB = 11 and the current input is x = 0?
    Show Answer

    Tracing it out, we have y=1.


  8. The propagation delays for all the combinational logic gates and the flip-flops are 2ns. The clock frequency is 100MHz. What is the worst case delay in nanosecond for the next states at A and B to appear (i.e. for A and B to be valid) after the input x is changed to be a valid input. Assume that the initial states AB are given and fixed.
    Show Answer

    From the frequency, we can compute the period of the clock to be 10ns.

    For the worst case delay, we need to consider the scenario that input x is propagated up to input of the register and it just missed the clk rise. It takes 4ns to propagate through the AND and OR gates, and another 10ns to wait for another clk rise. Finally, it takes 2ns to propagate through the register to produce A or B. Hence the worst case delay is 4+10+2 = 16ns.


  9. The propagation delays for all the combinational logic gates and the flip-flops are 2ns. Each dff have th and ts of 1ns each. If the clock frequency is not given, what is the maximum clock frequency (smallest clk period) that we can have for this device?

    Show Answer

    The clock period has to satisfy the feedback path (t2 timing constraint), that is made up with **tpd** of the dff, **tpd** of the AND gate, **tpd** of the OR gate, plus **ts** of the register. This adds up to 2+2+2+1 = 7ns. Hence the maximum frequency is:$$\frac{1}{(7*10^{-9})}= 142.9MHz$$.


  10. What are the output sequences from t=0 to t=15 of the circuit when fed the following input (fed from left to right): 1101 1111 1110 0010 from t=0 to t=15 respectively? Assume that the initial states are AB=00.
    Show Answer

    Given that the initial state is AB=00, that makes B = 1 at t=0. This is doable the tedious way by simply tracing the output y sixteen times from t=0 to t=15. We can also deduce from the functionality of the device, that is to detect three consecutive 1's and output 0 afterwards. The output sequence is therefore 0000 0011 1111 0000 from t=0 to t=15. repectively.

State-Machine Timing Computation (Intermediate)

Take a look at the following State Machine circuitry:

The device A2 has the following schematic:

It is made out of this device we call A000R with tcd = 1ns, and tpd = 3ns with the following schematic:

The truth table for A000R is as follows:

\[\begin{matrix} A & B & C & D & E \\ \hline 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ \hline \end{matrix}\]

The timing specifications for other devices in the state machine is:

  • The Mux has the following time specification: tcd = 1ns, and tpd = 2ns.
  • The Registers has the following time specification: tcd = 2ns, tpd = 5ns, ts = 2ns, th = 2ns.

Both A1 and A2 are combinational logic that contains A000R only. Unfortunately, the design for A1 is missing. We only know that A1 uses only A000R to compute the output and the next state function and that A1 has the same tpd as A2. The other information that we have is that the output of A1, X[2:0] is a sequence of decimal, [1, 2, 3, ... ] in the binary form, i.e. [001, 010, 011, ...].

Video explanation here.

Answer the following questions:

  1. How many bits should the constant Z1 have?
    Show Answer

    Since one of the inputs to the muxes are 3-bits, this hardware is implemented using three 2-input mux. Z1 is essentially three bits, connected to each of the three copies of 2-input muxes.


  2. How many bits should the constant Z2 have?
    Show Answer

    1 bit. The number of bits of each input to a combinational logic device such as A1 does not depend on anything else or other inputs.


  3. What is the decimal value of Z1?
    Show Answer

    Since X[2:0] produces an increasing sequence from decimal value of 1,2,3,4,... etc, we can easily guess that the the decimal value of Z1 should be 0, such that when there's a RESET, the output of the register R1 is zero.


  4. What is the decimal value of Z2?
    Show Answer

    Z2's decimal value is 1. The same reason applies: since the sequence X[2:0] produced by A1 is increasing by 1, the input to A1 should be 1 such that at *every* cycle, theres an addition of 1 to be produced at X.


  5. What is the tpd of A2 in nanosecond?
    Show Answer

    The **tpd** of A000R is 3ns, hence the **tpd** of A2 is 9ns since it is made out of three A000R modules connected in series.


  6. What is the minimum clock period in nanosecond?
    Show Answer

    The longest path that the clock period has to satisfy is R1 -> A1 -> A2 -> Z1 -> R2. Hence we need to consider the **tpd** of all devices in its path (except R2) plus **ts** of R2: 5+9+9+2+2 = 27ns.


  7. What is the minimum tcd of A1 in nanosecond such that th of input (Z2) can be 0?
    Show Answer

    **tcd** of A1 has to be large enough so as to satisfy **th** of R1. **th** of R1 is 2ns, and **tcd** of the mux is 1ns. Therefore min **tcd** of A1 is 2-1 = 1ns.


  8. What is value of A2’s tcd in nanosecond?
    Show Answer

    The **tcd** of A2 is basically the **tcd** of a single A000R (1ns) since that is the shortest path from any input to any output in A2.


  9. When RESET is 1 for several cycles, what will be the value of X[2:0]?
    Show Answer

    When RESET is 1, the output of R1 will be 000. Hence the value of X[2:0] will be 001..


  10. When X’s output is sequences of value [1, 2, 3, ...], what is the value of RESET?
    Show Answer

    RESET has to be 0 to enable the addition of the previous value of `X` to take effect, and form a new value of `X` in the next clock cycle.


Now, suppose that at time t=0, RESET signal is changed from 1 to 0, and X becomes 001. From then on, RESET remains 0:

  1. What is the decimal value of O[2:0] at time t = 0?
    Show Answer

    X is 001 and Y is 000 at t=0. Using the truth table of A000R and the schematic of A1, we can deduce that O[2:0]at t=0 is 1.


  2. What is the decimal value of O[2:0] at time t = 1?
    Show Answer

    X is 010 and Y is 001 at t=1. Using the truth table of A000R and the schematic of A1, we can deduce that O[2:0]at t=1 is 3.


  3. What is the decimal value of O[2:0] at time t = 3?
    Show Answer

    X is 011 and Y is 011 at t=2. Using the truth table of A000R and the schematic of A2, we can deduce that O[2:0]at t=3 is 2.


FSM Possibility (Basic)

We saw that certain functions, such as parentheses checking, cannot be performed by any finite state machine. Which of the following can be performed by an FSM?

Assume, in each case, that the device is to take a series of 0s and 1s that represent the digits of a binary number entered left to right.

  1. The device is to have a single output, which is 1 only under this specific condition: when the last 277 digits entered have been alternate 1s and 0s.
    Show Answer

    Yes. It is a bit tedious for `277` digits, but you should be able to sketch FSM for 3 or 4 digits.


  2. The device is to have a single output, which is 1 only under this specific condition: when more 0s than 1s have been entered.

    Show Answer

    No. Requires unbounded counting.


  3. The device is to have a single output, which is 1 only under this specific condition: when the number entered thus far is divisible by 3.

    Show Answer

    Yes, can be done by a 3-state machine.


  4. The device is to have a single output, which is 1 only under this specific condition: when an odd number of 1s and and even number of 0s have been entered.

    Show Answer

    Yes,, can be done with a 4-state machine.