50.002 Computation Structures
Information Systems Technology and Design
Singapore University of Technology and Design
Random Number Generation
Project
The code used for this tutorial can be found here.
Motivation
Many 50.002 projects would require you to generate random number sequences. However, our FPGAs cant do that. FPGAs are designed with deterministic logic, meaning their outputs depend entirely on their inputs and internal state. True randomness requires an external, inherently unpredictable source (e.g., thermal noise or quantum effects). As such, we can only produce pseudo-random numbers.
Pseudo-random refers to a sequence of numbers that appears random but is generated by a deterministic algorithm. Unlike truly random numbers, pseudo-random numbers are predictable if the algorithm and its initial state (seed) are known.
The pn_gen module
This module provided to you generates random number based on xorshift. It is a type of pseudo-random number generator (PRNG) that is simple, fast, and efficient (but shouldn’t be used in crypto applications). It works by repeatedly applying the XOR (exclusive OR) operation combined with bit shifts to a seed value to produce a sequence of pseudo-random numbers.
module pn_gen #(
// SEED needs to always be non-zero
// Since seed is XORed with the 32MSBs of SEED, we need the 96 LSBs to be nonzero.
SEED = 6781203480
)(
input clk, // clock
input rst, // reset
input next, // generate next number flag
input seed [32], // seed used on reset
output num [32] // "random" number output
) {
.clk(clk) {
dff x[32]
dff y[32]
dff z[32]
dff w[32]; // state storage
}
sig t [32]; // temporary results
always {
num = w.q; // output is from w
t = x.q ^ (x.q << 11); // calculate intermediate value
if (next) { // if we need a new number
x.d = y.q; // shift values along
y.d = z.q;
z.d = w.q;
// magic formula from Wikipedia
w.d = w.q ^ (w.q >> 19) ^ t ^ (t >> 8);
}
// Manually reset the flip-flops so we can change the reset value
if (rst) {
x.d = SEED[8:0];
y.d = SEED[15:9];
z.d = SEED[23:16];
w.d = SEED[31:24] ^ seed;
}
}
}
The initial SEED can be changed to any value that satisfies this condition: Out of the total 128 bits of the SEED, the least significant 96 bits of this SEED value must contain at least one 1 (i.e., they cannot all be 0). The 96 LSBs being non-zero ensures the generator has enough variability in its initial state to function correctly. Without this condition, the pseudo-random number generator may fail to produce meaningful outputs.
The input seed in the design is an additional input that provides external variability during the reset process. It is XORed with the most significant byte of the constant SEED during reset to initialize the state variable w.
Wrapping pn_gen module
This random_number_generator module wraps the pn_gen PRNG module and provides a higher-level interface for generating random numbers synchronized with a slower clock signal (slow_clk).
module random_number_generator#(
SIZE = 8
) (
input clk, // clock
input slow_clk,
input refresh,
output out[SIZE]
) {
dff seed[32](#INIT(0), .clk(clk))
pn_gen pn_gen(.clk(clk), .seed(seed.q))
edge_detector edge_detector(#RISE(1), #FALL(1), .clk(clk), .in(slow_clk))
always {
seed.d = seed.q + 1
pn_gen.rst = 0
pn_gen.next = 0
if (refresh){
pn_gen.rst = 1 // capture seed, generate fresh sequence
}
if (edge_detector.out){
pn_gen.next = 1
}
out = pn_gen.num[SIZE-1:0]
}
}
dff seed is a 32-bit seed register which increments continuously with each clock cycle (clk). It is used to re-initialize the PRNG when the refresh signal is asserted. This ensures that a unique seed is available for generating new sequences whenever the PRNG is reset.
An edge_detector monitors the slower clock (slow_clk) and generates a pulse on its edges. This pulse triggers the pn_gen to produce a new pseudo-random number synchronized with slow_clk. The module outputs the lower SIZE bits of the PRNG’s number, providing a clean interface for applications requiring synchronized and refreshed random number sequences.
Utilising random_number_generator
In alchitry_top.luc, we instantiate the random_number_generator and supply its inputs:
.clk(clk) {
reset_conditioner reset_cond
button_conditioner io_button_0(.in(io_button[0]), #CLK_FREQ(CLK_FREQ))
.rst(rst){
counter slow_clk(#SIZE(1), #DIV(CLOCK_DIVIDER))
}
edge_detector button_0_edge(#RISE(1), #FALL(0), .in(io_button_0.out))
random_number_generator generator(.slow_clk(slow_clk.value), .refresh(button_0_edge.out))
}
io_button[0] will refresh/start the sequence of the random number generator when pressed.
Observed Output
Here’s the observed output of the project:
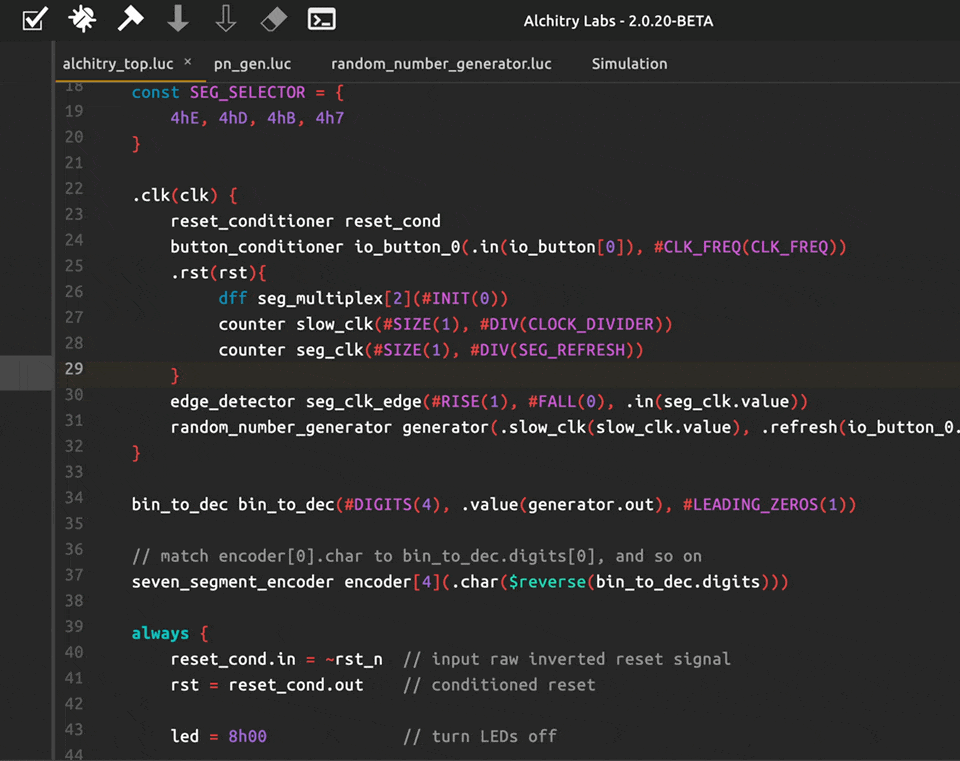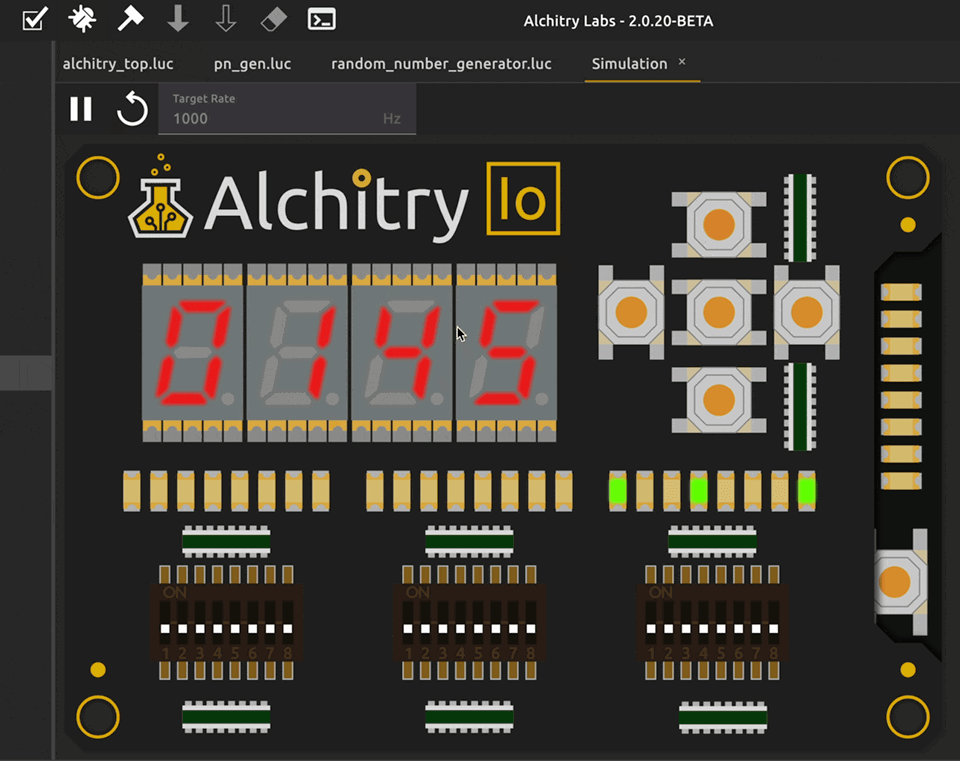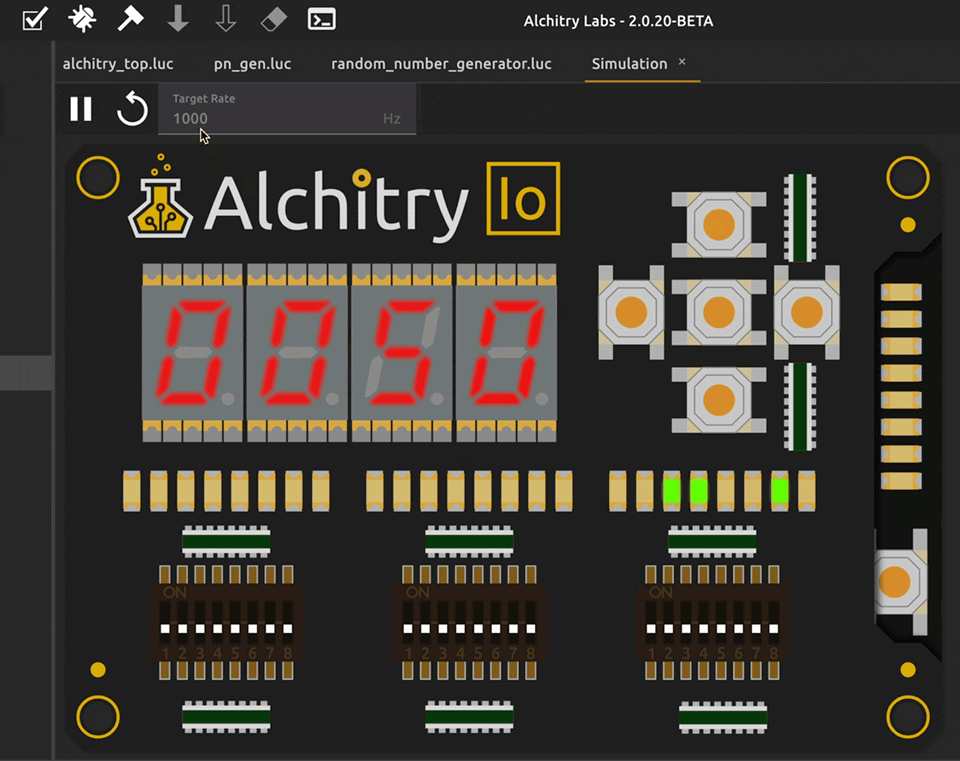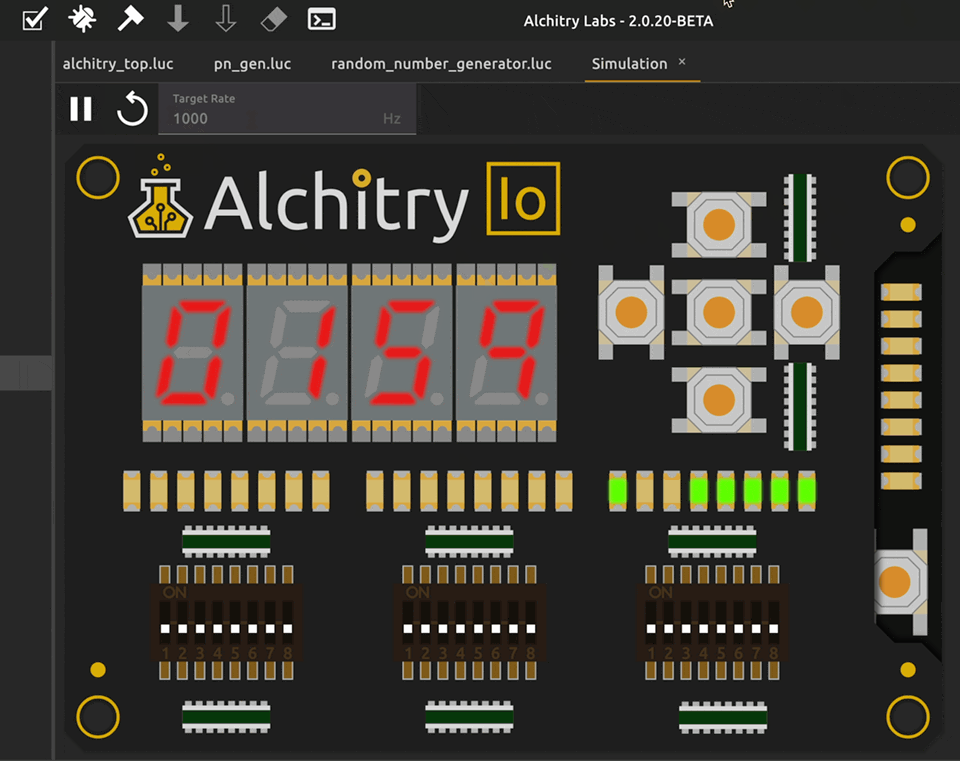
Varying generated number speed
The value CLOCK_DIVIDER in alchitry_top can be varied to control the speed of random_number_generator:
// alchitry_top.luc
const CLOCK_DIVIDER = $is_sim() ? 11 : 26
This is possible because CLOCK_DIVIDER directly affects slow_clk generated by the counter module, and its output slow_clk.value is used as slow_clk input of random_number_generator.
counter slow_clk(#SIZE(1), #DIV(CLOCK_DIVIDER))
random_number_generator generator(.slow_clk(slow_clk.value), .refresh(io_button_0.out))
Output Display
The number generated by random_number_generator is 8 bits long by default (SIZE is 8 in random_number_generator.luc). This value is displayed at io_led[0]:
// alchitry_top.luc
io_led[0] = generator.out
We improved the UI by utilising the 7segment module onboard. To do this, we need to first convert the binary value generator.out into decimal value using the bin_to_dec component. Afterwards, we need to multiplex the display of digits on the 7segment. We will not discuss how 7segment works in this tutorial. If you’re interested, please checkout this tutorial instead.
Summary
In this short tutorial, we learned how to generate a pseudo-random number using the FPGA.
We begin by writing the PRNG module pn_gen and then wrapping it to add additional control such as input seed and slow_clock to control the speed of number generation well as refreshing the generator’s state to produce new sequence of numbers.
This practice is common to modularize designs, allowing for reusable, maintainable, and easily extensible components that can be integrated into larger systems with additional functionality.
 50.002 CS
50.002 CS