Skip to main content Link Search Menu Expand Document (external link)
logo img  50.002 CS

50.002 Computation Structures
Information Systems Technology and Design
Singapore University of Technology and Design

The Digital Abstraction

Each topic’s questions are grouped into three categories: basic, intermediate, and challenging. You are recommended to do all basic problem set before advancing further.

VTC Plot (Basic)

The behavior of a 1-input 1-output device is measured by hooking a voltage source to its input and measuring the voltage at the output for several different input voltages, resulting in the following VTC plot,

We’re interested in whether this device can serve as a legal combinational device that obeys the static discipline. For this device, obeying the static discipline means that,

\[\begin{aligned} \text{If } V_{IN} &\leq V_{IL} \text{ then } V_{OUT} \geq V_{OH}, \\ \text{ and if } V_{IN} & \geq V_{IH} \text{ then } V_{OUT} \leq V_{OL} \end{aligned}\]

When answering the questions below, assume that all voltages are constrained to be in the range of 0V to 5V,

  1. Can one choose a Vol of 0V for this device? Explain.
  2. What is the smallest voltage that the device can produce?
  3. Assuming that we want to have 0.5V noise margins for both “0” and “1” values, what are the appropriate voltage levels for Vol, Vil, Vih, and Voh so that the device obeys the static discipline? Hint: there are many choices. Just choose the one that obeys the static discipline and the NM constraint.
  4. What device is this called?
Show Answer

  1. No. From the plot, it can be seen that **Vout** can never reach below 0.5V. If **Vol** is chosen to be 0V, then the device doesn't satisfy the static discipline anymore.
  2. 0.5V. That is the lowest amount of **Vout** that the device can produce.
  3. We can choose: $$V_{OL} = 0.5V$$ from the graph, since the device is capable of producing such low voltage. With NM of 0.5V, that means that: $$V_{IL} = V_{OL} + 0.5V = 1V$$ From the graph, we can also choose: $$V_{OH} = 4V$$ as the part with the highest gain in the middle of the graph can most probably be the forbidden zone. Therefore, $$V_{IH} = V_{OH} - 0.5V= 3.5V$$
  4. This device is an **inverter**, since a **high** input produces a **low** output and vice versa.


Inverter Madness (Intermediate)

(a). The following graph plots the VTC for a device with one input and one output. Can this device be used as a combinational device in logic family with 0.75V noise margins?

Video explanation here.

Show Answer

No. This device gain is not more than 1, hence it cannot be used as a combinational device.


(b). You are designing a new logic family and trying to decide on values of the four parameters: Vol, Vil, Vih, and Voh that lead to non-zero noise margins for various possible inverter designs. Four proposed inverter designs exhibit the VTC shown in the diagrams below. For each design, either specify four suitable values of Vol, Vil, Vih, and Voh or explain why no values can obey the static discipline.

Hint: you may want to start by choosing Noise Immunity to be between 0.2V to 0.5V for ease of computation.

Video explanation here.

Show Answer

(B) and (C) cannot be used as inverter (combinational device) as its absolute gain is less than 1.

For (A), choose Noise Immunity = 0.5V, then: $$V_{OL} = 1V, V_{IL} = 1.5V, V_{IH} = 5V, V_{OH} = 5.5V$$

For (D), choose Noise Immunity = 0.3V, then: $$V_{OL} = 0.2V, V_{IL} = 0.5V, V_{IH} = 5, V_{OH}= 5.5V$$


Static Discipline (Basic)

(a). Consider a combinational buffer with one input and one output. Suppose we set its input to some voltage \(V_{IN}\), wait for the device to reach a steady state, then measure the voltage on its output Vout and find out \(V_{OUT} < V_{OL}\). What can we deduce about the value of \(V_{IN}\)?

Show Answer

We have a valid low output, but that doesnt mean that we have a valid low input. However we know for sure that input cannot be higher than **Vih** because static discipline requires the output to be higher than **Voh** if this is the case for a buffer.

Hence, the only thing we can infer is that:$$V_{IN} < V_{IH}$$ This means input voltage can **either** be a valid low *or* an invalid value.


(b). Now consider an inverter. Suppose we set its input to some voltage \(V_{IN}\), wait for the device to reach a steady state, then measure the voltage on its output Vout, and find \(V_{OUT} > V_{OH}\). What can we deduce about the value of \(V_{IN}\)?

Show Answer

We have a valid high output, but that doesnt mean that we have a valid low input. Static discipline states that given a valid input, the device is always able to give a valid output, but it does not mean that the reverse is true, i.e: invalid input does NOT have to give out invalid output.

However we do know for sure that the input cannot be higher than **Vih** because static discipline requires the output to be lower than **Vol** if this is the case for an inverter. Hence, the only thing we can infer is that: $$V_{IN} < V_{IH}$$ This means input voltage can **either** be a valid low *or* an invalid value.


VTC Analysis (Intermediate)

Take a look at the figure below.

Which of the following specification(s) does not obey the static discipline? Select all that apply.

  1. \[V_{IL} = 0.4V, V_{IH} = 3.1V, V_{OL} = 0.2V, V_{OH} = 4.2V\]
  2. \[V_{IL} = 0.5V, V_{IH} = 3V, V_{OL} = 0.3V, V_{OH} = 4V\]
  3. \[V_{IL} = 0.2V, V_{IH} = 3V, V_{OL} = 0.4V, V_{OH} = 4.2V\]
  4. \[V_{IL} = 0.5V, V_{IH} = 4V, V_{OL} = 0V, V_{OH} = 3.5V\]
  5. \[V_{IL} = 0.5V, V_{IH} = 3.5V, V_{OL} = 0V, V_{OH} = 4V\]

Video Explanation here.

Show Answer

None of them obey the static discipline. You may easily check whether the device is able to provide the prescribed **Voh** given a corresponding **Vih** in the options, and whether it is able to provide as well the given **Vol** given a coresponding **Vil** in the options from tracing the graph.


Choosing Signaling Thresholds (Intermediate)

The following are VTCs of a single-input single-output devices to be used in a project:

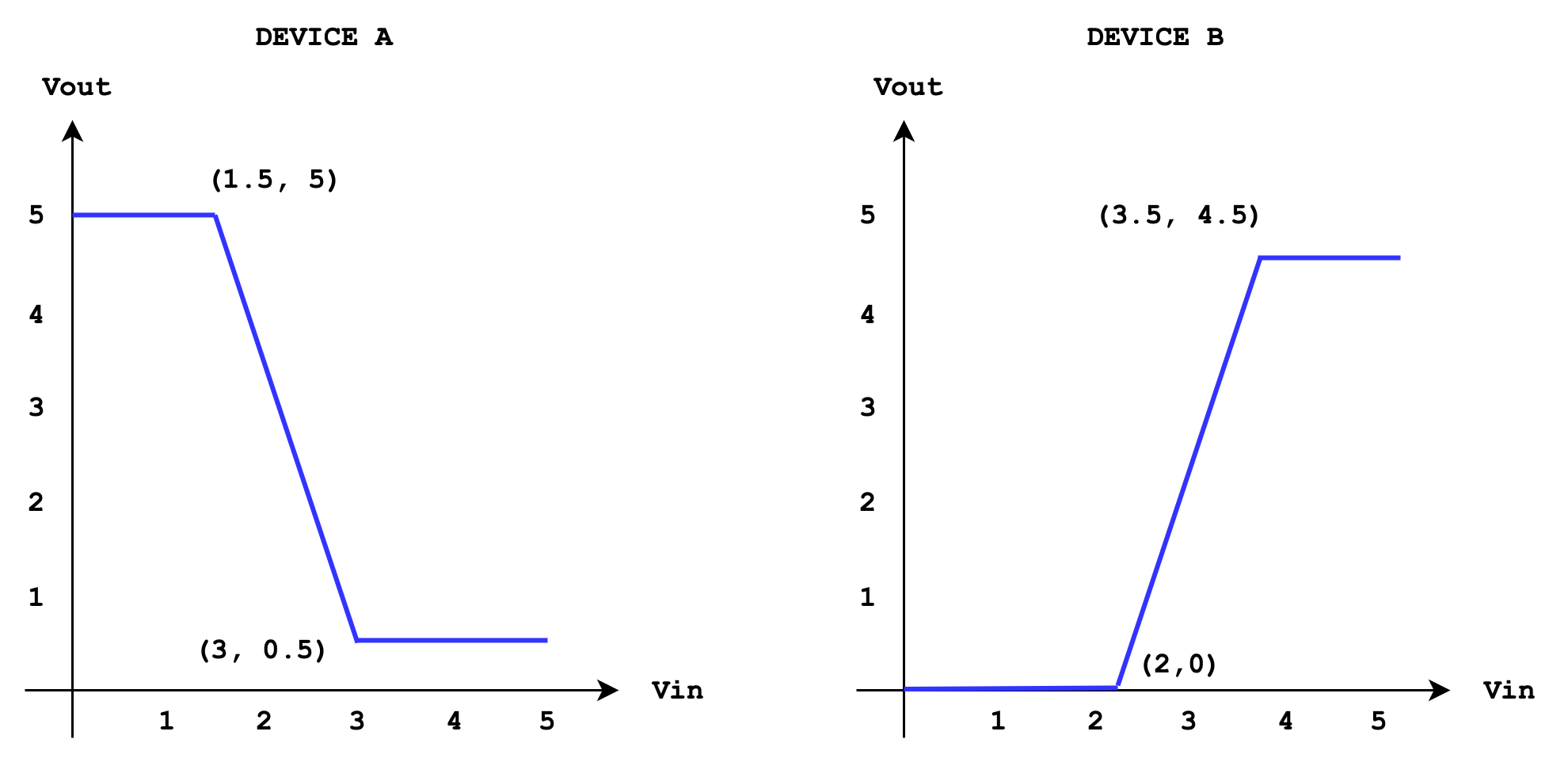
Choose a single set of signaling threshold: Vol, Vil, Vih, Voh to be used with both devices to give the best noise immunity possible.

Video explanation here.

Show Answer

The four values are: Vol = 0.5V, Vil = 1.5V, Vih = 3.5V, and Voh = 4.5V. This results in low noise margin and high noise margin of 1V. The noise immunity is therefore 1V.