50.005 Computer System Engineering
Information Systems Technology and Design
Singapore University of Technology and Design
Natalie Agus (Summer 2024)

Python Cryptography

In NS Module 3, we examined how the security properties of confidentiality and data integrity could be protected by using symmetric key cryptography and signed message digests. In this lab exercise, you will learn how to write a program that makes use of 3DES for data encryption, SHA256 for creating message digests and RSA for digital signing.

At the end of this lab exercise, you should be able to:

Understand how symmetric key cryptography can be used to encrypt data and protect its confidentiality.
Understand how multiple blocks of data are handled using different block cipher modes and padding.
Compare the different block cipher modes in terms of how they operate.
Understand how hash functions can be used to create fixed-length message digests.
Understand how public key cryptography (e.g., RSA algorithm) can be used to create digital signatures.
Understand how to create message digest using hash functions (e.g., MD5, SHA-1, SHA-256, SHA-512, etc) and sign it using RSA to guarantee data integrity.

There are 3 parts of this lab:

Symmetric key encryption for a text file
Symmetric key encryption for an image file
Signed message digests

System Requirements

The starter code provided to you is written in Python. You need at least Python 3.10 to complete this assignment and the cryptography module. We will use the Python cryptography module to write our program instead of implementing 3DES, RSA and SHA-256 directly. You will also need this module for your Programming Assignment 2, so take this lab as a precursor to the asssignment.

While you can develop in Python using any OS, this lab is tested to run on a POSIX-compliant OS (path, etc is resolved) so it is not guaranteed that it will run on other OS. You need to fix OS-specific problems in the starter code by yourself.

Starter Code

Download the starter code:

git clone https://github.com/natalieagus/nslab2.git

This will result in a directory with the following structure:

nslab2
   |-original_files
      |-longtext.txt
      |-shorttext.txt
      |-SUTD.bmp
      |-triangle.bmp
   |-.gitignore
   |-1_encrypt_text.py
   |-2_encrypt_image.py
   |-3_sign_digest.py
   |-README.md
   |-requirements.txt

Then, cd to nslab2 and install the required modules:

python3 -m pip install -r requirements.txt

In this lab, you’re only required to modify all the 3 python files. When you’re done, submit your code via our Telegram bot as usual, and answer the questionnaire on eDimension as usual. There are areas labeled in these .py files as TODO, and these are your tasks.

Test the Starter Code

Running the three .py files at this point should give you the following printouts stating that you havent implemented the relevant tasks:

Debug Notes

Invalid Syntax

Some of you might encounter the error when running python3 [starter-code].py

  match convert_bytes_to_int(read_bytes(client_socket, 8)):
        ^
      case 0:

SyntaxError: invalid syntax

That’s because your python3 is NOT aliased to python3.10 or that you don’t have python3.10 installed. Fix this on your own. You’re a CS major student. Not knowing how to install Python and manage its libraries is a really really bad thing; it’s like as if the entire 50.002 and the first 6 weeks of CSE doesn’t mean anything to you.

In this handout, we assume that python3 is always aliased to python3.10.

That is, if you type python3 in the terminal, you’ll see at least version 3.10 printed out:

Module Not Found

Some of you might encouter the error ModuleNotFoundError: No module named ‘cryptography’. You should know what you need to do by now as a CS student. If you have installed cryptography using pip install cryptography, but still suffer from this error, it simply means that the pip you used does not install to the path library of whatever python3 version you are using right now. That is, you may have mixed up Python and pip versions on your machine.

Assuming your python3 is aliased to python3.10, then you can do the following as stated above, instead of pip3 install -r requirements.txt you copy pasted from somewhere.

python3 -m pip install -r requirements.txt

Submission

Once you have completed 1_encrypt_text.py, 2_encrypt_image.pym 3_sign_digest.py.py, zip all files and submit your answer to our bot. Just type /start and follow the instruction there. Don’t forget to head to eDimension and complete the lab questionnaire as usual.

Text Encryption

Symmetric encryption is a type of encryption where only one key (a secret key) is used to both encrypt and decrypt a message. There are many symmetric key encryption algorithms: AES, 3DES, Blowfish, Rivest Cipher 5, etc. For this task, we are going to specifically use a 128-bit AES in CBC mode but we aren’t going to build it from scratch. We will be using Fernet, a recipe that provides symmetric encryption and authentication to data. It is a part of the cryptography library for Python, which is developed by the Python Cryptographic Authority (PYCA).

You can read more about Fernet’s full documentation and its specs, but that’s out of scope for this lab. We just want to use it as a tool to perform symmetric key encryption.

Open 1_encrypt_text.py and let’s begin.

Overview

There are two methods in the file, enc_text(input_filename, output_filename) and dec_text(input_filename, output_filename).

Quickly study what it does.

If you scroll below, you’ll find these methods called repeteadly to encrypt and decrypt various files:

if __name__ == "__main__":
    enc_text("original_files/shorttext.txt", "output/enc_shorttext.txt")
    dec_text("output/enc_shorttext.txt", "output/dec_shorttext.txt")

    enc_text("original_files/longtext.txt", "output/enc_longtext.txt")
    dec_text("output/enc_longtext.txt", "output/dec_longtext.txt")

Our goal is to perform symmetric key encryption to plaintext files, and save it as encrypted files (with prefix enc). Then, take these encrypted files, decrypt it, and save it back to disk (with prefix dec).

Key Generation

Task 1-1

TASK 1-1: Generate a fresh fernet key.

This key is used to both encrypt and decrypt messages. You need to keep this safe in real applications. Any adversaries that can get access to this key will be able to decrypt all your supposedly confidential messages.

You can use the following method, and print it out to inspect its value.

symmetric_key = Fernet.generate_key()
print(symmetric_key)

Cipher Instantiation

A cipher is name given in general that represents an algorithm for performing encryption or decryption. The key above is used as an input to the cipher to perform encryption or decryption.

Task 1-2

TASK 1-2: Generate a cipher using Fernet (in both enc and dec functions)

You can take the symmetric key above and generate an instance of Fernet to help you encrypt and decrypt later:

cipher = Fernet(symmetric_key)

Encryption and Decryption

At this stage, encryption and decryption is trivial. You can encrypt data (in bytes) and decrypt data (in bytes) using the following method:

message_bytes = b'Lorem ipsum dolor sit amet, consectetuer adipiscing elit, sed diam nonummy nibh euismod tincidunt ut laoreet dolore magna'
encrypted_message_bytes = cipher.encrypt(message_bytes)
decrypted_message_bytes = cipher.decrypt(encrypted_message_bytes)
assert message_bytes == decrypted_message_bytes

Now you should be able to complete these two tasks.

Task 1-3

TASK 1-3: Encrypt the raw bytes. Fill in your answer under the TODO for this task.

Fernet Token

encrypted_message_bytes, known as the ciphertext or the Fernet token in this context (as we are using the Fernet protocol in this Python’s cryptography module), contains a few things in this order:

Version: 1 byte

Timestamp: 8 bytes

IV: 16 bytes (the initialization vector)

Ciphertext: Variable length (the actual encrypted data)

HMAC: 32 bytes (the message authentication code)

Task 1-4

TASK 1-4: Decrypt the raw bytes. Fill in your answer under the TODO for this task.

Creating a Printable Text Using base64

If you attempt to print the encrypted message bytes directly, you might see some weird characters printed out. That’s because they’re no longer represent any printable encoding.

In enc_text function, we provide a way to encode the encrypted byte into a printable string using the base64 module, before saving it to file.

   # Convert the ciphertext output to a printable string
   encrypted_base64_bytes = base64.b64encode(encrypted_bytes)
   encrypted_text = encrypted_base64_bytes.decode("utf8")

   # Save the printable string back to file
   with open(output_filename, "w") as fp:
      fp.write(encrypted_text)

This way you can open the enc_[output_filename] and read the encrypted bytes as proper string.

As a result, when decrypting later on, we need to decode it back first before performing a decryption. We have done this for you in dec_text function:

   # Open the file containing the cyphertext, read as string
   with open(input_filename, "r") as fp:
      encrypted_text = fp.read()

   # Convert the printable string back to bytearray
   encrypted_bytes = base64.b64decode(encrypted_text.encode("utf8"))

You may experiment writing the encrypted bytes to the file directly without encoding, and observe the difference.

Note about Encoding

This section is just for your information as there seems to be rampant misunderstanding that encoding and encryption are both the “same” thing just because they transform data from one format to another.

Encoding != Encryption. Encoding schemes and encryption algorithms serve fundamentally different purposes, even though both involve transforming data from one form to another. The key distinctions lie in their objectives, methods, and the necessity for secrecy.

Encoding is designed to transform data into a specific format for efficient transmission or storage, making it convenient to process by computers and human-readable in some cases. Encoding does not aim to keep information secret but ensures that it is represented in a form suitable for various systems or applications. Common examples of encoding include Base64, ASCII, and Unicode.

Encryption, on the other hand, is intended to protect data confidentiality by converting the original information (plaintext) into an unreadable format (ciphertext) using an algorithm and a secret key. The primary purpose of encryption is to ensure that only authorized parties can access the original information by decrypting the ciphertext using the correct key. Examples of encryption algorithms include AES (Advanced Encryption Standard), RSA (Rivest-Shamir-Adleman), and DES (Data Encryption Standard).

Encoding Schemes

Encoding schemes are methods used to represent data in specific formats, often for the purposes of data storage, transmission, and interpretation by computers and human operators. Here are examples of common encoding schemes, categorized by their primary use:

Textual Data Encoding:

ASCII (American Standard Code for Information Interchange): Uses 7 bits to represent 128 characters, including English letters, digits, and control characters. It’s the basis for many other encoding schemes.
ISO-8859-1 (Latin-1): Extends ASCII to 8 bits, adding support for Western European languages by including characters such as ñ, ç, and ß.
UTF-8, UTF-16, UTF-32 (Unicode Transformation Formats): Variable-length encodings that can represent every character in the Unicode character set, accommodating all known characters and symbols from languages around the world.

Numeric Data Encoding:

Binary: The most basic form of encoding, representing data in two states, 0 and 1, directly corresponding to the off and on states of a computer’s transistors.
Hexadecimal (Hex): Uses base 16, representing numbers using sixteen distinct symbols, 0-9 to represent values zero to nine, and A-F to represent values ten to fifteen.

Media Data Encoding:

Base64: Encodes binary data into characters selected from a set of 64, using the letters A-Z, a-z, the numbers 0-9, and characters + and /. It is used to encode binary data in contexts that primarily or solely handle textual data, like embedding images in HTML or email attachments.
MIME (Multipurpose Internet Mail Extensions): An extension of the email protocol that supports sending non-text attachments like audio, video, images, and application programs.

Data Compression and Archiving:

ZIP: A file format that supports lossless data compression. A ZIP file may contain one or more files or directories that may have been compressed.
GZIP: A file format and a software application used for file compression and decompression. GZIP is often used in combination with TAR for archiving files.

Data Integrity and Security:

MD5 (Message Digest Algorithm 5): A widely used cryptographic hash function producing a 128-bit (16-byte) hash value, typically expressed as a 32-character hexadecimal number. It’s used to check the integrity of files.
SHA (Secure Hash Algorithm) family: Cryptographic hash functions that can generate a hash value (digest), including SHA-1, SHA-256, and SHA-512, differing in their bit length and security level. Used for secure data transmission and digital signatures.

Each of these encoding schemes serves specific purposes, from basic representation of text and numbers to complex data integrity and security.

Encoding schemes use a publicly known method for transforming data, while encryption algorithms require a secret key for both encrypting and decrypting the data.

Image Encryption

In this task, we are going to encrypt an image with another symmetric key cryptography called the 3-DES. The 3-DES applies the DES cipher algorithm three times to each data block.

Data Encryption Standard (DES) was a US encryption standard for encrypting electronic data. It makes use of a 56-bit key to encrypt 64-bit blocks of plaintext input through repeated rounds of processing using a specialized function. Note that the DES 56-bit key is no longer considered adequate in the face of modern computing.

In 2016, a major security vunerability in DES and 3DES was revealed. As a result, NIST (National Institute of Standards and Technology) depcrecated DES and 3DES for all applications by 2023. It has been replaced by AES which is more secure and more robust.

Nevertheless, we are going to experiment using 3-DES for this task and observe how image encryption brings about different issues.

Open 2_encrypt_image.py and let’s begin.

Overview

There are 5 helper functions in the file, and these are mainly used to read columns of an image as bytes. You may leave these untouched:

image_to_cols(image)
cols_to_image(cols)
col_to_bytes(col, top_down=False)
tuple_to_bytes(x)
bytes_to_col(x, length, top_down=False)

The main bulk of your task involves filling up the TODO in enc_img function. If you scroll down, you will see it being called with various images as input.

Loading the Image

The image is loaded in enc_img as such:

# Load the image
im = Image.open(input_filename)

We will encrypt this image column by column.

Yes we can encrypt the whole image as a flattened array, or row by row, but for the sake of this lab we will do it column by column so that we can observe a special output.

Loading Pixel Values per Column

However, we can’t use it directly for our encryption. We need to first convert it to an array of columns. As such, this helper function image_to_cols is used. This is not a Python class, but here’s what zip and * does:

# arr is a 3 by 2 by 3 matrix (3 rows, 2 columns)
arr = [
         [(1, 2, 3), (4, 5, 6)],
         [(7, 8, 9), (10, 11, 12)],
         [(13, 14, 15), (16, 17, 18)],
      ]
cols = list(zip(*arr))
print("cols", cols)

The above has the output:

# Note: cols is a 2 by 3 by 3 matrix (each "row" here is a column value of arr)

cols = [
         ((1, 2, 3), (7, 8, 9), (13, 14, 15)),
         ((4, 5, 6), (10, 11, 12), (16, 17, 18)),
       ]

The * operator in this context unpacks the elements of arr and provides them as separate arguments to the zip function like zip([(1, 2, 3), (4, 5, 6)], [(7, 8, 9), (10, 11, 12)], [(13, 14, 15), (16, 17, 18)]).

Convert Columns to Bytes

The columns in the image consists of pixel values (tuples of 3 integers, representing RGB values), and we can’t encrypt it straight away without converting them to bytes. The helper function col_to_bytes and tuple_to_bytes already did this for you:

def col_to_bytes(col, top_down=False):
    """
    Helper function to convert each pixel tuple to bytes. Iterate the column top-down or bottom-up
    """
    out = []
    for pixel in col[:: (1, -1)[top_down]]:
        out.insert(0, tuple_to_bytes(pixel))
    return b"".join(out)


def tuple_to_bytes(x):
    """
    Helper function to convert a tuple of integers into bytes
    """
    return int.from_bytes(list(x), byteorder="big").to_bytes(
        3, byteorder="big"
    )

In short, if a pixel in col has the value of (255, 255, 255) (RGB), it will be converted into 3 bytes: b'\xff\xff\xff'. All pixels in the column will be converted into bytes and joined together, for instance:

cols = [
         ((1, 2, 3), (7, 8, 9), (13, 14, 15)),
         ((4, 5, 6), (10, 11, 12), (16, 17, 18)),
       ]

for col in cols:
    column_bytes = col_to_bytes(col, True)
    print("column_bytes", column_bytes)

Has the output:

column_bytes b'\x01\x02\x03\x07\x08\t\r\x0e\x0f'
column_bytes b'\x04\x05\x06\n\x0b\x0c\x10\x11\x12'

Bottom-up vs Top-down

We can load the column bytes bottom-up or top-down. This will affect our encryption result later on. Consider our example above with image matrix:

arr = [
         [(1, 2, 3), (4, 5, 6)],
         [(7, 8, 9), (10, 11, 12)],
         [(13, 14, 15), (16, 17, 18)],
      ]

The output above loads the column bytes “top-down”, so we have column bytes:

column_bytes b'\x01\x02\x03\x07\x08\t\r\x0e\x0f' # (1,2,3), (7,8,9), (13,14,15) in bytes
column_bytes b'\x04\x05\x06\n\x0b\x0c\x10\x11\x12' # (4,5,6), (10,11,12), (16,17,18) in bytes

If we load the column bytes “bottom-up”, we will end up with column bytes:

column_bytes b'\r\x0e\x0f\x07\x08\t\x01\x02\x03' # (13,14,15), (7,8,9), (1,2,3) in bytes
column_bytes b'\x10\x11\x12\n\x0b\x0c\x04\x05\x06' # (16,17,18), (10,11,12), (4,5,6) in bytes

Notice how the order within the tuple must be preserved, just the way we pack each tuple is different. Don’t worry, we have already done these mental gymnastics for you.

Key Generation

The key in this case is already given to you:

    # Key for 3DES
    key = b"\xb6\x11\xd5\xd7\x83\xb2,m"

Create a Cipher

Task 2-1

TASK 2-1: create a cipher with TripleDES using the key above.

cipher = Cipher(algorithms.TripleDES(key), mode)

The constructor for Cipher takes in two arguments:

The first argument specifies the algorithm to be used and the key
The second argument, mode, specifies how multiple blocks of data are handled by the encryption algorithm. It can be either ECB or CBC depending on whether the input argument cbc to enc_image is True or False.

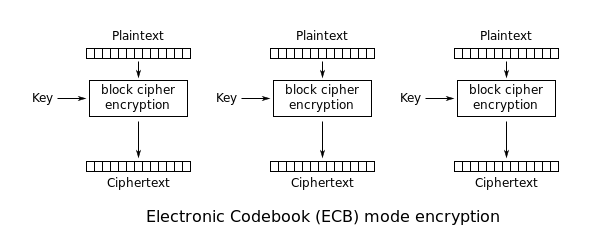
ECB Mode

ECB stands for ‘electronic codebook’. When using ECB mode, identical input blocks always encrypt to the same output block.

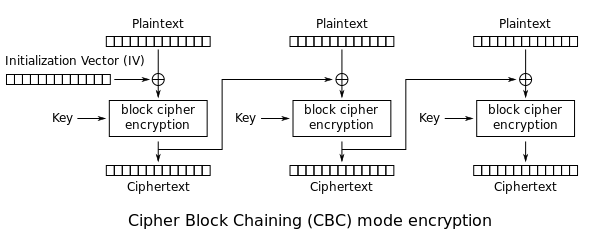
CBC Mode

CBC stands for ‘cipher block chaining’. In CBC mode, the current block is added to the previous ciphertext block, and then the result is encrypted with the key (thus the word chained). Decryption is thus the reverse process, which involves decrypting the current ciphertext and then adding the previous ciphertext block to the result.

Initialization Vectors (IVs)

IVs are used in encryption to ensure that the same plaintext encrypted with the same key will result in different ciphertexts each time. This randomness is crucial for security in modes like CBC. An IV is generated for each encryption operation and is typically included with the ciphertext to be used during decryption.

They don’t have to be secret. The security of encryption does not rely on the secrecy of the IV. Instead, it relies on the secrecy of the symmetric key. The IV’s purpose is to introduce randomness to ensure that identical plaintexts do not produce identical ciphertexts.

In protocols like Fernet above, the IV is included with the ciphertext. When decrypting, the IV is extracted from the token and used to decrypt the data.

Create a CipherContext instance for encryption

Task 2-2

TASK 2-2: Afterwards, create a CipherContext instance from the encryptor() method

encryptor = cipher.encryptor()

It can be used to encrypt data as such:

raw_bytes = b"abcdefghijklmnop"  # 16 bytes
print("raw_bytes", raw_bytes)
encrypted_bytes = (
    encryptor.update(raw_bytes) + encryptor.finalize()
)  # 16 bytes
print("encrypted_bytes", encrypted_bytes)

The output is:

raw_bytes b'abcdefghijklmnop'
encrypted_bytes b'\x12\x96]\x00\x12\x0e\x80C*\x1b\xc7d\xd2\x10=\xeb'

Note that if ECB mode is used, then the encrypted bytes above will always be the same.

However, if we change the length of raw_bytes into 17 bytes, eg: b"abcdefghijklmnopq", we will be faced with ValueError: The length of the provided data is not a multiple of the block length.. What happened?

Pad Column Bytes

Task 2-(3,4)

TASK 2-(3,4): If you attempt to encrypt your data right away with this, it will fail because 3DES encrypts 64 bit blocks. It expects the length of the data to be encrypted to be a multiple of 64.

Hence we need to pad it. At first you need to create a padding instance, and use it as such:

padder = padding.PKCS7(64).padder()
test_bytes = b"Lorem" # 5 bytes
padded_test_bytes = padder.update(test_bytes) + padder.finalize() # 8 bytes
print("padded_test_bytes", padded_test_bytes)

The output is:

padded_test_bytes b'Lorem\x03\x03\x03'

PKCS7 padding is a generalization of PKCS5 padding (also known as standard padding). PKCS7 padding works by appending N bytes with the value of chr(N) (Python built-in function chr), where N is the number of bytes required to make the final block of data the same size as the block size.

With this, you should be able to complete Task 2-3 and 2-4.

Task 2-5

TASK 2-5: Encrypt the padded column bytes. Fill in your answer under the TODO for this task.

Observe the Output Images

When you have successfully completed Task 2-1 to 2-5, there will be 8 output images at output/. Observe them and think about the answers to these questions.

Look at all ECB outputs.

Are there any differences between top-down and bottom-up output?
What kind of security vulnerabilities the ECB mode has? Will you use this to encrypt your images in real life?

Then look at all CBC outputs:

Compare the result of CBC mode with ECB mode, what differences do you see? Is it an improvement (more secure)?
Why do you think the outputs have the “smearing” effect?
Does it still have some kind of security vulnerabilities?
Do we want to prioritise top-down or bottom-up encryption, or will it depend on the image?

Message Digest

In class, we also learned how a signed message digest could be used to guarantee the integrity of a message. Signing the digest instead of the message itself gives much better efficiency.

In the final task, we will create and sign a message digest, and verify it with the corresponding public key.

Open 3_sign_digest.py and let’s begin.

Generate RSA Key-Pair

Task 3-(1,2)

TASK 3-(1,2): Before we can sign any digest, we need to first generate the asymmetric key pair.

private_key = rsa.generate_private_key(
    public_exponent=65537,
    key_size=1024,
)

public_key = private_key.public_key()

The first argument dictates the value of e (the public exponent). Almost everyone uses 65537 (for security purposes) as recommended here. The second argument dictates the key size (1024 bits in for this task).

Using the Keys

Afterwards, we can use the private or public key for encryption or decryption. However, there are some terminologies that you need to know.

Encrypt and Decrypt

Encryption of a message with a public key is normally labeled as encryption in the API, and decryption with a private key is labeled as decryption (names that you will expect). Here’s an example to get you started:

data_bytes = b"Lorem ipsum dolor sit amet"

encrypted_data_bytes = public_key.encrypt(
    data_bytes,
    padding.OAEP(
        mgf=padding.MGF1(hashes.SHA256()),
        algorithm=hashes.SHA256(),
        label=None,
    ),
)

decrypted_data_bytes = private_key.decrypt( # 128 bytes long
    encrypted_data_bytes,
    padding.OAEP(
        mgf=padding.MGF1(hashes.SHA256()),
        algorithm=hashes.SHA256(),
        label=None,
    ),
)

assert decrypted_data_bytes == data_bytes

print("encrypted_data_bytes", encrypted_data_bytes) # ciphertext
print("decrypted_data_bytes", decrypted_data_bytes) # same as data_bytes

Note that for encrypt with public_key, the length of data bytes depends on the padding scheme. This example uses OAEP scheme, but there are other schemes too such as PKCS1v15, etc. You can read more about alternative paddings and their parameters here.

It is important to know how many bytes the padding will add at minimum.

With 1024 RSA-key, the maximum length of message that it can encrypt is also 1024 bits (128 bytes)
OAEP with SHA-256 takes 66 bytes of padding overhead, leaving you with only 62 bytes of content to encrypt/decrypt at a time
You will encounter this as well in Programming Assignment 2

Sign and Verify

If you want to encrypt a message using the private key, the keyword you should look for in the API is sign, and the output is commonly called as a signature:

Conversely, if you want to decrypt the output signature, the keyword in the API is verify. There will be no output here if the verification succeeds (the decrypted signature matches the initial message), but a VerficationError will be raised if otherwise.
But don’t be fooled! Verification is a decryption, and signing is an encryption. They just have different names that are tied to their purpose.

Here’s an example to get you started:

data_bytes = b"Lorem ipsum dolor sit amet, consectetuer adipiscing elit, sed diam nonummy nibh euismod tincidunt ut laoreet dolore magna" # 121 bytes

signature = private_key.sign(
    data_bytes,
    padding.PSS(
        mgf=padding.MGF1(hashes.SHA256()),
        salt_length=padding.PSS.MAX_LENGTH,
    ),
    hashes.SHA256(),  # Algorithm to hash the file_data before signing
)

try:
    public_key.verify(
        signature,
        data_bytes,
        padding.PSS(
            mgf=padding.MGF1(hashes.SHA256()),
            salt_length=padding.PSS.MAX_LENGTH,
        ),
        hashes.SHA256(),
    )
    print("Verification Succeeds")
except:
    print("Verification Fails")
    exit()

Note that the length of data_bytes can be arbitrarily long because it will be hashed automatically (third argument of sign) before encrypted with the private key. The output length of SHA-256 is 32 bytes only (256 bits) which when added with the padding, will still be less than 128 bytes.

We also use a different padding scheme for the signature (PSS) and not OAEP because of the nature of the padding. You may read more about it here or in any other online source materials but it is our of our syllabus.

Salting in Hashing

A salt is a random value added to the input (e.g., a password) before hashing.

It ensures that the same input will produce different hash outputs. This prevents attackers from using precomputed hash tables (rainbow tables) to reverse-engineer the hashed values.

Characteristics of Salt:

Uniqueness: Each input (e.g., each password) should have a unique salt to prevent identical inputs from producing the same hash.
Randomness: The salt should be randomly generated to ensure unpredictability.
Non-Secret: The salt does not need to be kept secret. It is typically stored alongside the hash in a database. From Lab 3 (TOCTOU), you have seen how salt is kept alongside the hashed password in /etc/shadow file.

Creating a Digest

Task 3-(3,4)

TASK 3-(3,4): In order to create a message digest, you must first create a hash instance, then use it with update(input) and finalize() methods.

data_bytes = b"Lorem Ipsum" # 11 bytes

hash_function = hashes.Hash(hashes.SHA256())

hash_function.update(data_bytes)
message_digest_bytes = hash_function.finalize() # 32 bytes
print("message_digest_bytes", message_digest_bytes)

The print output is:

message_digest_bytes b'\x03\r\xc1\xf96\xc3AZ\xff?3W\x165\x15\x19\r4z(\xe7X\xe1\xf7\x17\xd1{\xaeE5A\xc9'

Question

Is the length of message_digest_bytes always the same (32 bytes), regardless of the length of the input data_bytes?

Task 3-(5-8)

TASK 3-(5-8): With all the explanations above, you should be able to complete these tasks. Fill in your answer under the TODO for this task.

Summary

Finally, if you scroll below you will find these four function calls:

if __name__ == "__main__":
    enc_digest("original_files/shorttext.txt")
    enc_digest("original_files/longtext.txt")
    sign_digest("original_files/shorttext.txt")
    sign_digest("original_files/longtext.txt")

Here we test encryption of digest using public key (enc_digest) and encryption of digest using private key (sign_digest), and we test each with two files of differing length. Study its output carefully and head to edimension to answer the rest of the questionnaires.