• TOC

50.002 Computation Structures
Information Systems Technology and Design
Singapore University of Technology and Design
Modified by: Kenny Choo, Natalie Agus, Oka Kurniawan (2021)

Lab 1: CMOS

Starter Code

The following files inside your /50002/ folder are what you’re going to open and modify or study for this lab, then submit (unless otherwise stated):

  • lab1_submit.jsim

You need to head to edimension to answer a bunch of questionnaire there for this lab.

The lecture notes on Digital Abstraction and CMOS Technology are closely related to this lab.

Task A and Task B: Studying the effect of MOSFET “ON” and MOSFET “OFF”.
Related Notes: CMOS Technology

Task C and Task D: finding optimal VTC
Related Notes: Digital Abstraction

Task E and Task F: tcd and tpd
Related Notes: CMOS Technology

  • Timing Specifications of Combinational Logic Devices
  • Actually measure tpd and tcd from raw plots (input and output timing of a given gate or circuitry) to understand by heart why we need these timing specifications to obey static discipline
  • This is on the contrary to classroom exercises where we give you the tpd and tcd of each gate and simply do the math to compute the tpd and tcd of a given circuit

Task G: logic synthesis and CMOS circuit
Related Notes: Logic Synthesis

Introduction to JSim

(you really should’ve read this intro section before coming to class)

In this lab, we will be using a simulation program, JSim, to make measurements of an N-channel MOSFET (or NFET for short). JSim uses mathematical models of circuit elements to make predictions of how a circuit will behave both statically (DC analysis) and dynamically (transient analysis). The model for each circuit element is parameterised, e.g., the MOSFET model includes parameters for the length and width of the MOSFET, as well as many parameters that characterize the physical aspects of the manufacturing process. For the models we are using, the manufacturing parameters have been derived from measurements taken at the integrated circuit fabrication facility, and so the resulting predictions are quite accurate.

The (increasingly) complete JSim documentation can be found here. But we will try to include pertinent information for JSim in each lab writeup.

Download and extract 50002.zip (link in our **course handout**), open it and simply double-click the `jsim.jar` for this lab. For some newer OS like MacOS Monterey, path to Desktop and Documents **may be protected** and old Java programs like our `jsim` and `bsim` **will not even have access** to view files in these paths. This means you won't be able to open the template files. If this happens, you should place the 50002 folder in your `home` or `Downloads` directory instead.


User Interface

Overview of the JSim user interface

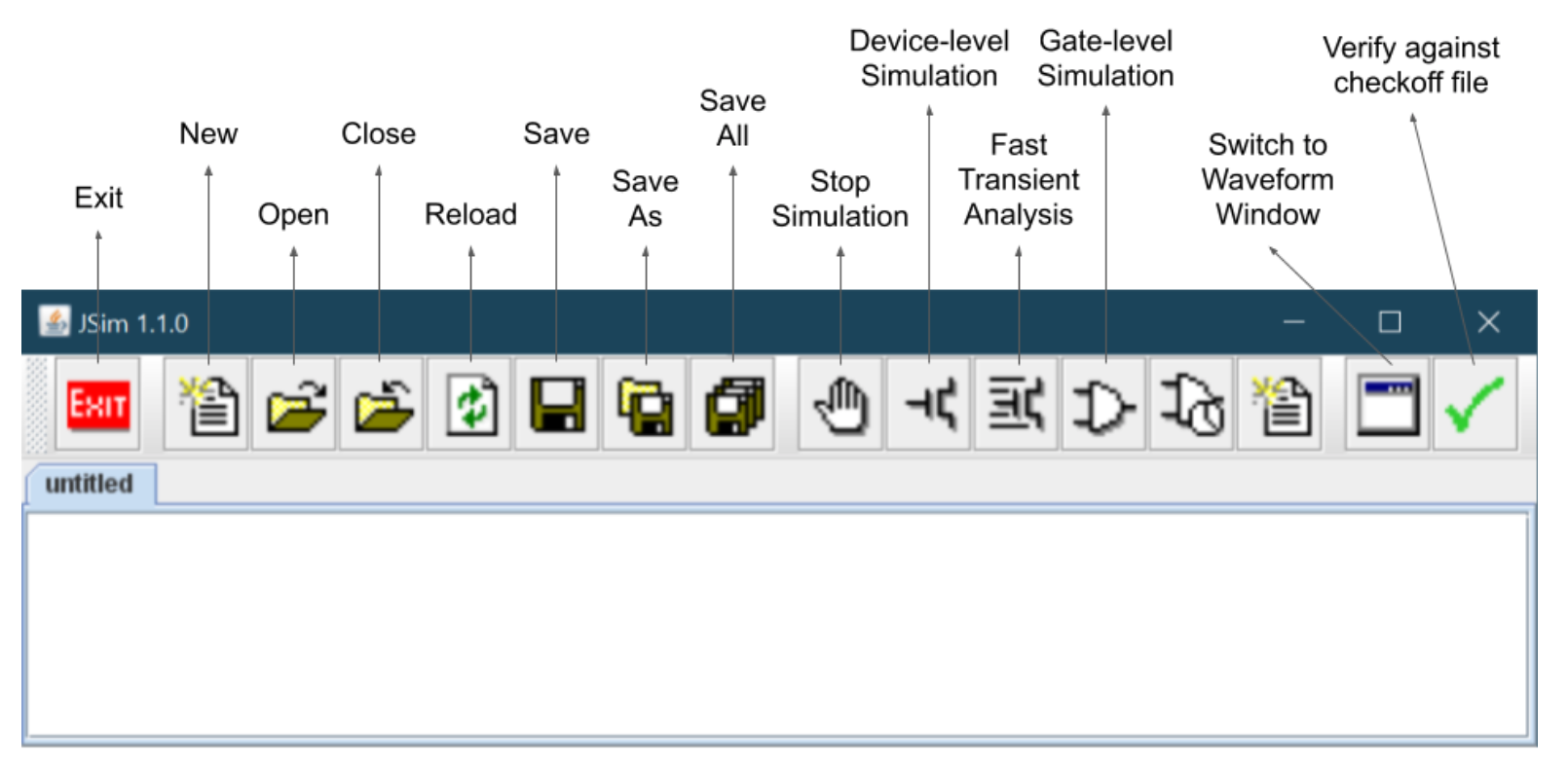
Each icon means as follows:

Waveform Window

The waveform window shows various waveforms in one or more “channels.” Initially one channel is displayed for each .plot control statement in your netlist. If more than one waveform is assigned to a channel, the plots are overlaid on top of each using a different drawing color for each waveform. If you want to add a waveform to a channel simply add the appropriate signal name to the list appearing to the left of the waveform display (the name of each signal should be on a separate line). You can also add the name of the signal you would like displayed to the appropriate .plot statement in your netlist and rerun the simulation. If you simply name a node in your circuit, its voltage is plotted. You can also ask for the current through a voltage source by entering I(Vid).

The waveform window has several other buttons on its toolbar: waveform button

You can zoom and pan over the traces in the waveform window using the controls found along the bottom edge of the waveform display. The scrollbar at the bottom of the waveform window can be used to scroll through the waveforms. You can recentre the waveform display about a particular point by placing the cursor at that position and pressing c.

JSim netlist format

The JSim netlist format is quite similar to that used by SPICE, a well-known circuit simulator. Each line of the netlist is one of the following:

  • Comment line
    • Indicated by an “*” (asterisk) as the first character.
    • Comment and blank lines are ignored when JSim processes your netlist
    • C++/Java style comments can also be used
    • “//”, all characters starting with this and to the end of the line are ignored.
    • “/” and “/”, any lines or parts of lines enclosed by these are ignored.

  • Continuation line
    • Indicated by a “+” as the first character.
    • Treated as if they had been typed at the end of the previous line (without the “+” of course)
    • No limit to length of an input line, but breaking long lines using “+” makes it easier to edit and understand
    • “+” also continues comment lines

  • Control statement
    • Indicated by “.” (period) as the first character.
    • Provides information about how the circuit is to be simulated

  • Circuit element
    • Indicated by a letter as the first character, that represents the type of circuit element. e.g. “r” for resistor, “c” for capacitor, “m” for MOSFET, “v” for voltage source.
    • Remainder of line specifies which circuit nodes connect to which device terminals and any parameters needed by that type of circuit element. For example, the following line describes a 1000Ω resistor called “R1” that connects to nodes A and B: R1 A B 1k

Note that the numbers can be entered using engineering suffixes for readability. Common suffixes are:

  • kilo: “k” = 1000
  • micro: “u” = 1E-6
  • nano: “n” = 1E-9
  • pico: “p” = 1E-12

Part 1: Characterising MOSFETs (45 mins)

Make some measurements of an NFET by hooking it up to a couple of voltage sources to generate different values for VGS and VDS. Our end goal is to obtain the VTC plot of the NFET. Recall that we learn this in the Digital Abstraction chapter in our lecture.

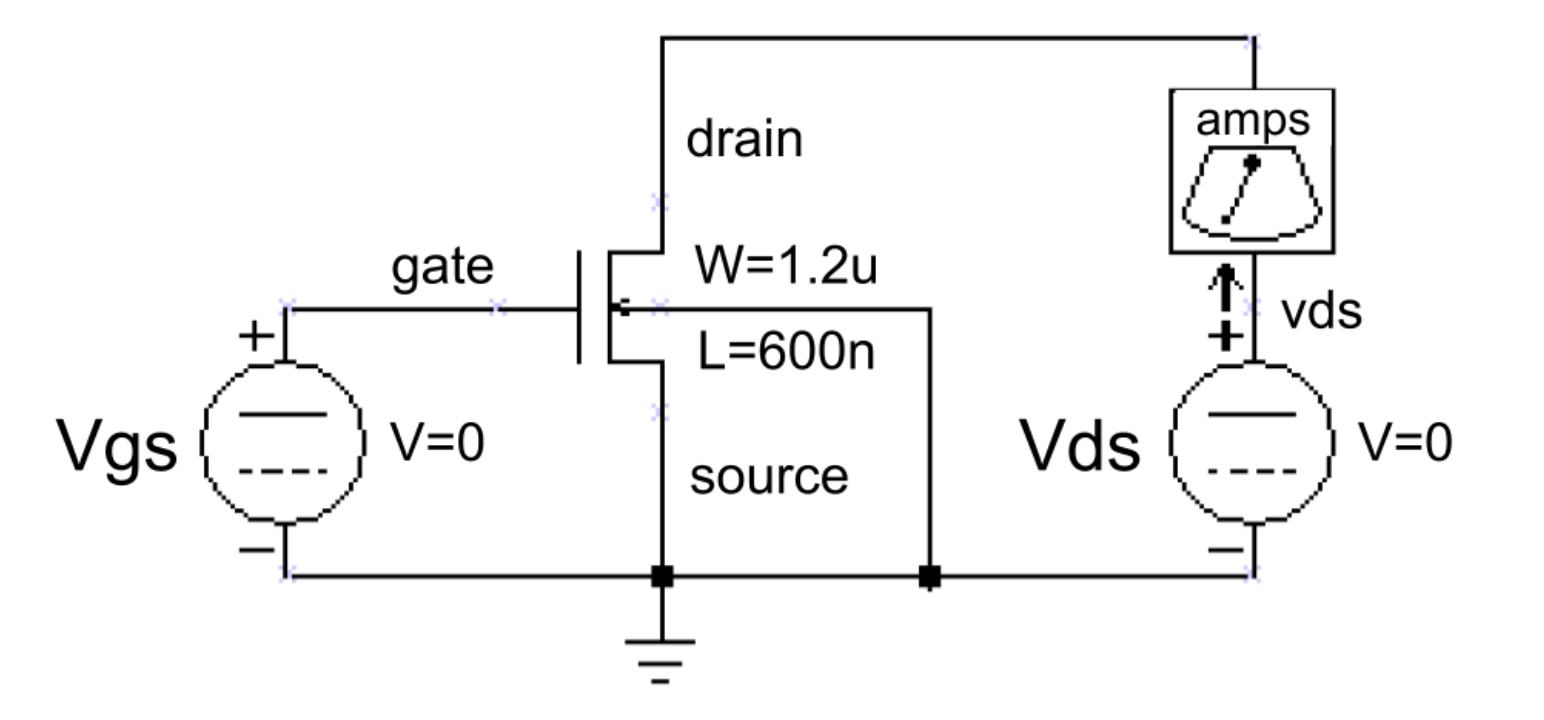
The setup to characterise our NFET is as follows: setupnfet

We have included an ammeter (built from a 0V voltage source) so we can measure IDS, the current flowing through the MOSFET from its drain terminal to its source terminal. Here’s the translation of the above schematic into our netlist format:

1
2
3
4
5
6
7
8
9

* plot Ids vs. Vds for 5 different Vgs values
.include "nominal.jsim"
Vmeter vds drain 0v
Vds vds 0 0v
Vgs gate 0 0v
* N-channel MOSFET used for our test
M1 drain gate 0 0 NENH W=1.2u L=600n
.dc Vds 0 5 .1 Vgs 0 5 1
.plot I(Vmeter)
Line Description
1, 6 A comment. Any line that begins with a * signifies a comment.
2 A control statement that directs JSim to include a netlist file containing the MOSFET model parameters for the manufacturing process we will be targeting this semester. The pathname shown MUST be MODIFIED to point at where your nominal.jsim file is located
3-5 These specify three voltage sources; each voltage source specifies the two terminal nodes and the voltage we want between them. Note that the reference node for the circuit (marked with a GROUND symbol in the schematic) is always called 0. The v following the voltage specification is not a legal scale factor and will be ignored by JSim–it is included just to remind ourselves that the last number is the voltage of the voltage source. All three sources are initially set to 0 volts but the voltage for the Vds and Vgs sources will be changed later when JSim processes the .dc control statement. We can ask JSim to plot the current through voltage sources which is how we’ll see what Ids is for different values of Vgs and Vds. We could just ask for the current of the Vds voltage source, but the sign would be wrong since JSim uses the convention that positive current flows from the positive to negative terminal of a voltage source. So we introduce a 0V source with its terminals oriented to produce the current sign we’re looking for.
7 This is the MOSFET, where we have specified in order the names of the drain, gate, source and substrate nodes (in this order!). The next item names the set of model parameters JSim should use when simulating this device; “NENH” for an NFET, and “PENH” for a p-channel MOFET (PFET). The final two entries specify the width and length of the MOSFET. Note that the dimensions are in microns (1E-6 meters) since we’ve specified the “u” scale factor as a suffix. Do not forget the “u” or your MOSFETS will be meters long! You can always use scientific notation (e.g., 1.2E-6) if suffixes are confusing.
8 A control statement requesting a DC analysis of the circuit made with different settings for the Vds and Vgs voltage sources: the voltage of Vds is swept from 0V to 5V in .1V steps, and the voltage of Vgs is swept from 0V to 5V in 1V steps. Altogether \(51 \times 6\) separate measurements will be made.
9 A control statement that gets JSim to plot the current through the voltage source named “Vmeter”. JSim knows how to plot the results from the dual voltage sweep requested on the previous line: it will plot I(Vmeter) vs. the voltage of source Vds for each value of voltage of the source Vgs—there will be 6 plots in all, each consisting of 51 connected data points.



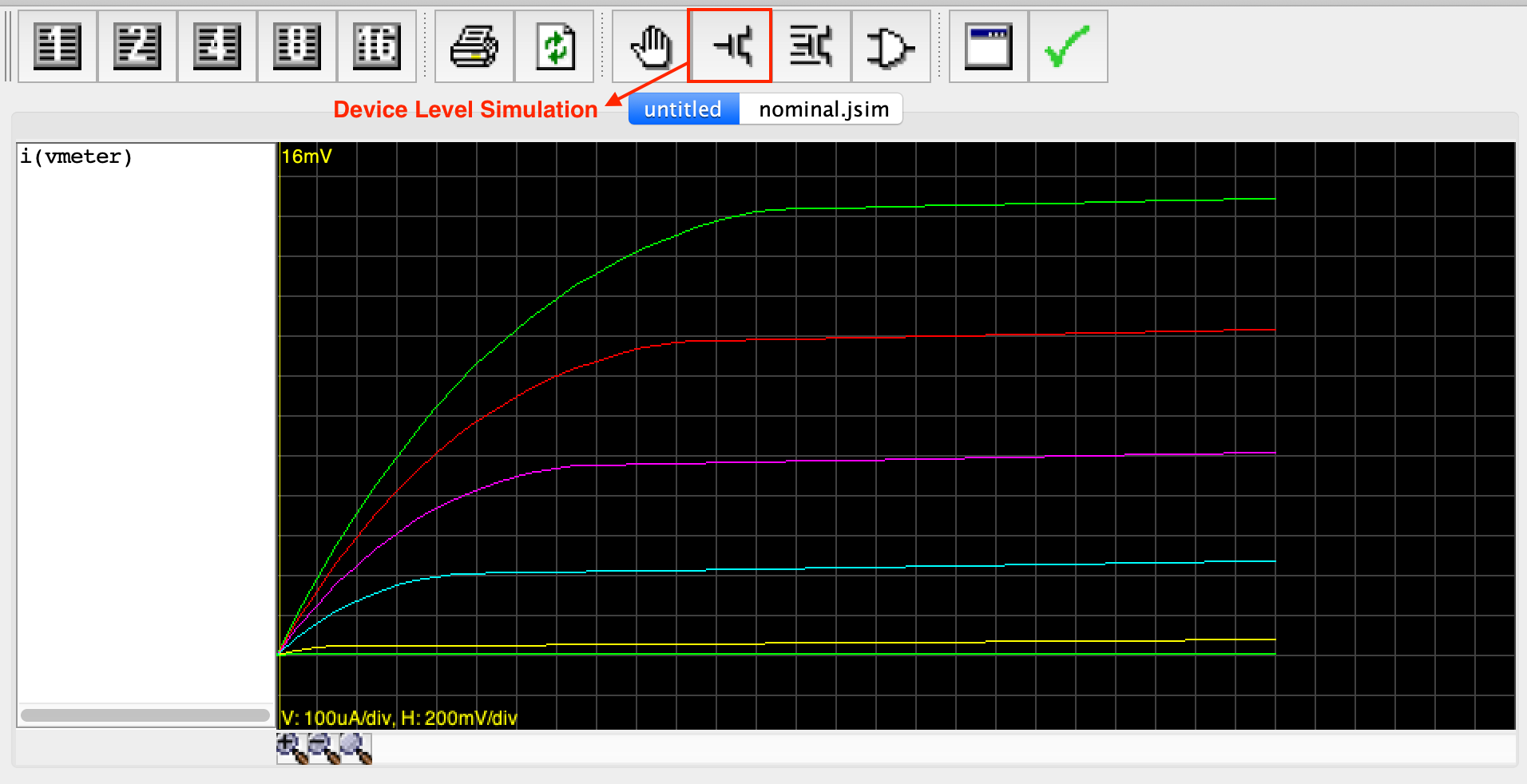
After you enter the netlist above, you might want to **save** your efforts for later use by using the “**save file**” button. To run the simulation, **click** the “**device-level simulation**” button on the toolbar.


After a pause, a waveform window will pop up and we can take some measurements.

  • As you move the mouse over the waveform window, a moving cursor will be displayed on the first waveform above the mouse’s position and a readout giving the cursor coordinates will appear in the upper left hand corner of the window.
  • To measure the delta (difference) between two points, position the mouse so the cursor is on top of the first point. Now click left and drag the mouse (i.e., move the mouse while holding its left button down) to bring up a second cursor that you can then position over the second point.
  • The readout in the upper left corner will show the coordinates for both cursors and the delta between the two coordinates.
  • You can return to one cursor by releasing the left button.

Making Measurements on the MOSFETS

Task A: MOSFET “on” Effective Sheet Resistance

To get a sense of how well the channel of a turned-on MOSFET conducts, let us estimate the effective resistance of the channel while the MOSFET is in the linear conduction region. We’ll use the Vgs = 5V curve (the upper-most plot in the window) . The equation at the linear region is given by:

\[\begin{align} I_D = \mu_n C_{ox} \frac{W}{L} \left[(V_{GS} - V{th}) V_{DS} - \frac{V_{DS}^2}{2} \right] (1+\lambda V_{DS}) \end{align}\]

The actual effective resistance is given by \(\delta V_{DS}/\delta I_{DS}\) and clearly depends on which VDS we choose .

Let’s use VDS = 1.2V on the VGS = 5 curve.

We could determine the resistance graphically from the slope of a line tangent to the IDS curve at VDS = 1.2V. But we can get a rough idea of the channel resistance by determining the slope of a line passing through the origin and the point we chose on the IDS curve, i.e., compute channel resistance \(\approx 1.2V / \delta I_{DS}\).

Of course, the channel resistance depends on the dimensions of the MOSFET we used to make the measurement.

For MOSFETs, their \(I_{DS}\) is proportional to W/L where W is the width of the MOSFET (1.2 microns in this example) and L is the length (0.6 microns in this example) of the MOSFET. Refer to this notes if you can’t visualise which is the width and length of the MOSFET.

When reporting the effective channel resistance, it’s useful to report the sheet resistance, i.e., the resistance when W/L = 1. That way you can easily estimate the effective channel resistance for other size devices by scaling the sheet resistance appropriately.

Since W/L = 2 for the device you measured, it conducts twice as much current and has half the channel resistance as a device with W/L = 1, so you need to double the channel resistance you computed above in order to estimate the effective channel sheet resistance.

**Record** down the value for the effective channel sheet resistance you calculated from that measurement. You need this information to get Checkoff 1. You can access the checkoffs 1 to 7 for Lab 1 through eDimension.


Task B: MOSFET “off” Leakage Current

Now let us see how well the MOSFET turns “off.” Take some measurements of IDS at various points along the VGS=0V curve (the bottom-most plot in the window).

Notice that they are not zero! MOSFETs do conduct minute amounts of current even when officially “off”, a phenomenon called “subthreshold conduction”. While negligible for most purposes, this current is significant if we are trying to store charge on a capacitor for long periods of time (this is what DRAMs try to do).

Make a measurement of IDS when VGS=0V and VDS=2.5V.

  • Based on this measurement report how long it would take for a .05pF capacitor to discharge from 5V to 2.5V, i.e., to change from a valid logic “1” to a voltage in the forbidden zone.
  • Recall from Physics II (10.005) that Q = CV, so we can estimate the discharge time as t=CV/IOFF.
  • So if our MOSFET switch controls access to the storage capacitor, you can see we will need to refresh the capacitor’s charge at fairly frequent intervals.
**Record** down the estimated discharge time. You will need this information for Checkoff 2.


Part 2: Noise Immunity (45 mins)

Setup and Introduction

Defining Circuit Elements Using “.subckt”

Create a new file and paste the following code. The following JSim netlist shows you how to define your own circuit elements using the “.subckt” statement:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

* circuit for Lab#1, Task C thru F
.include "nominal.jsim"

* 2-input NAND: inputs are A and B, output is Z
.subckt nand2 a b z
MPD1 z a 1 0 NENH sw=8 sl=1
MPD2 1 b 0 0 NENH sw=8 sl=1
MPU1 z a vdd vdd PENH sw=8 sl=1
MPU2 z b vdd vdd PENH sw=8 sl=1
.ends

* INVERTER: input is A, output is Z
.subckt inv a z
MPD1 z a 0 0 NENH sw=16 sl=1
MPU1 z a vdd vdd PENH sw=16 sl=1
.ends

The “.subckt” statement introduces a new level of netlist.

  • All lines following the “.subckt” up to the matching “.ends” statement will be treated as a self-contained subcircuit.
  • This includes model definitions, nested subcircuit definitions, electrical nodes and circuit elements.
  • Remember the order of mosfet node declaration: drain gate source substrate(bulk)
    • MPD1 z a 1 0 NENH sw=8 sl=1 signifies that drain is connected to node z, gate to node a, source to node 1 (this is NOT VDD) bulk to node 0 (ground)
    • Notice how the source node of MPD1 is connected to the drain node of MPD2, which means that both NFETs are connected in series
    • Both PFETs are connected in parallel (by CMOS rule)

The only parts of the subcircuit visible to the outside world are its terminal nodes which are listed following the name of the subcircuit in the “.subckt” statement:

1
2
3

.subckt name terminals…
* internal circuit elements are listed here
.ends

In the example netlist, two subcircuits are defined:

  • nand2 which has 3 terminals named “a”, “b” and “z” inside the nand2 subcircuit
  • inv which has 2 terminals named “a” and “z”.

Using Subcircuits

Once the definitions are complete, you can create an instance of a subcircuit using the “X” circuit element:

1

Xid nodes… name

where name is the name of the circuit definition to be used, id is a UNIQUE name for this instance of the subcircuit and nodes… are the names of electrical nodes that will be hooked up to the terminals of the subcircuit instance.

There should be the same number of nodes listed in the “X” statement as there were terminals in the “.subckt” statement that defined name.

For example, here’s a short netlist that instantiates 3 NAND gates (called “g0”, “g1” and “g2”):

1
2
3

Xg0 d0 ctl z0 nand2
Xg1 d1 ctl z1 nand2
Xg2 d2 ctl z2 nand2

Explanation:

  • The node ctl connects to all three nand2 gates instances; all the other terminals are connected to different nodes.
  • Note that any nodes that are private to the subcircuit definition (i.e., nodes used in the subcircuit that don’t appear on the terminal list) will be unique for each instantiation of the subcircuit (like local variables)
    • For example, there is a private node named 1 used inside the nand2 definition.
    • When JSim processes the three “X” statements above, it will make three independent nodes called “xg0.1”, “xg1.1” and “xg2.1”, one for each of the three instances of nand2.
    • There is no sharing of internal elements or nodes between multiple instances of the same subcircuit.
    • The example netlist above uses vdd (jsim standard for **POWER SOURCE) whenever a connection to the power supply is required.

Shared Nodes

There are two common shared nodes in jsim: vdd and 0. Please do not use these to name your custom electrical nodes.

It is sometimes convenient to define nodes that are shared by the entire circuit, including subcircuits; for example, power supply nodes. The ground node “0” is such a node; all references to “0” anywhere in the netlist refer to the same electrical node. The included netlist file nominal.jsim defines another shared node called “vdd” using the following statements:

1
2

.global vdd
VDD vdd 0 3.3v

The example netlist above allows us to use vdd whenever a connection to the power supply is required.

Symbolic Dimensions

The other new twist introduced in the example netlist is the use of symbolic dimensions for the MOSFETs (“SW=” and “SL=”) instead of physical dimensions (“W=” and “L=”). Symbolic dimensions specify multiples of a parameter called SCALE, which is also defined in nominal.jsim:

1

.option SCALE=0.6u

So with this scale factor, specifying “SW=8” is equivalent to specifying “W=4.8u.”

Using symbolic dimensions is encouraged since it makes it easier to determine the W/L ratio for a MOSFET (the current through a MOSFET is proportional to W/L) and it makes it easy to move the design to a new manufacturing process that uses different dimensions for its MOSFETs. Note that in almost all instances “SL=1” since increasing the channel length of a MOSFET reduces its current carrying capacity, not something we’re usually looking to do.

We’ll need to keep the PN junctions in the source and drain diffusions reverse biased to ensure that the MOSFETs stay electrically isolated, so the substrate terminal of NFET (those specifying the “NENH” model) should always be hooked to ground (node 0). Similarly the substrate terminal of PFET (those specifying the “PENH” model) should always be hooked to the power supply (node vdd).

Task C: Optimising Noise Margins

To maximize noise margins we want to have the transition in the voltage transfer characteristic (VTC) of the nand2 gate centered halfway between ground and the power supply voltage (3.3V)

Why? Ask yourself, and review the lecture on digital abstraction.

To determine the VTC for nand2, we’ll perform a dc analysis to plot the gate’s output voltage as a function of the input voltage using the following additional netlist statements. Paste this under the nand2 and inverter declaration you made above in the new file.

1
2
3
4
5
6
7
8
9

* dc analysis to create VTC
Xtest vin vin vout nand2
Vin vin 0 0v

Vol vol 0 0.3v
Voh voh 0 3v

.dc Vin 0 3.3 .005
.plot vin vout voh vol

Run the device-level simulation, and the following window should appear:

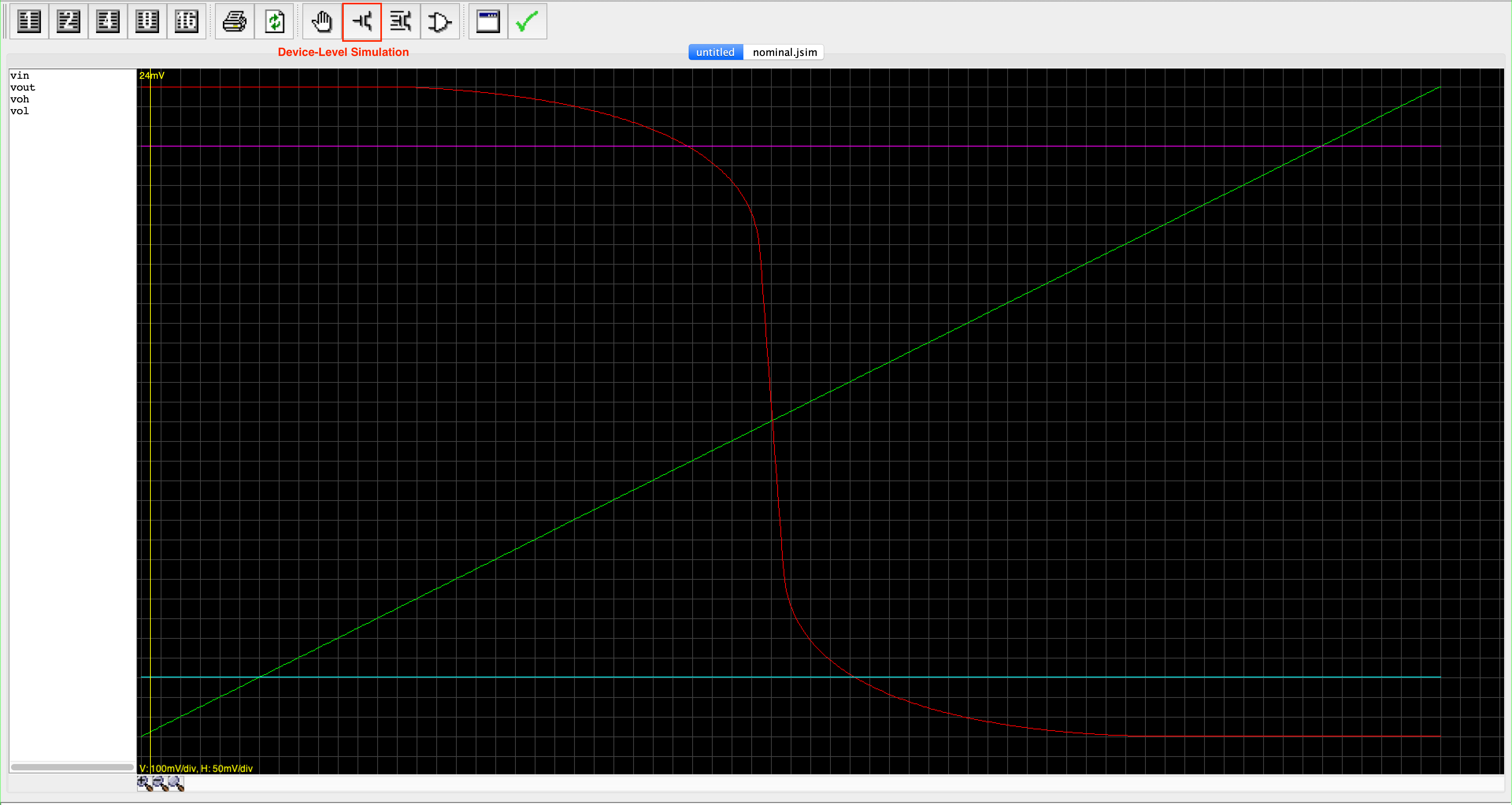
  • To maximise the noise margin, we need to center the VTC transition. One possible way is to adjust the size of the NFET in the nand2 definition as SW=8 SL=1 and adjust the width (SW) of both pFETs until the plots for vin and vout (green and red line) intersect at about 1.65 volts. Keep the SL of the pFETs the same.
    • You can also adjust SW, SL of both NFET and PFET as you wish, but we save you that guessing game and give you the most optimal setting right away.
  • Just try different integral widths (i.e, 9, 10, 11, …) for the value of SW of the pFETs in the nand2 definition.
  • Report the integral width that comes closest to having the curves intersect at 1.65V.
**Record** down the SW value you found. You will need this information for Checkoff 3.


Task D: Finding Noise Immunity

Keep the SW value you found in Task C for the rest of this lab!

The noise immunity of a gate is the smaller of the low noise margin (Vil - Vol) and the high noise margin (Voh - Vih).

If we specify VOL = 0.3V and VOH = 3.0V, what is the largest possible noise immunity we could specify and still have the “improved” NAND gate of part (C) be a legal member of the logic family?

**Record** down the noise immunity value. You will need this information for Checkoff 4.


Hint:

  • To measure the low noise margin, use the VTC to determine what VIN has to be in order for VOUT to be 3V, and then subtract VOL (0.3V) from that number.
  • To measure the high noise margin, use the VTC to determine what VIN has to be in order for VOUT to be 0.3V, and then subtract that number from VOH (3.0V).
  • We’ve added some voltage sources corresponding to VOL and VOH (which lines of the code was it?) to make it easier to make the measurements on the VTC plot.

Note: make these measurements using your “improved” nand2 gate that has the centered VTC, i.e., with the updated widths for the PFETS.

Part 3: Contamination and Propagation delays (45 mins)

Now that we have the MOSFETs ratioed properly to maximize noise immunity, let’s measure the contamination time (tc) and propagation time (tp) of the nand2 gate.

The contamination delay, **tcd**, for the `nand2` gate will be a **lower** bound for all the tc measurements we make. Similarly, the propagation delay, **tpd**, for the `nand2` gate will be an **upper** bound for all the tP measurements.


Recall that the contamination delay is the period of output validity after the inputs have become invalid. That means there are four scenarios, depending on the combination of input and output values:

  • The period of output remaining at valid 1 (before falling to valid 0 eventually) after input that was previously at valid 1 has turned invalid
  • The period of output remaining at valid 1 (before falling to valid 0 eventually) after input that was previously at valid 0 has turned invalid
  • The period of output remaining at valid 0 (before rising to valid 1 eventually) after input that was previously at valid 1 has turned invalid
  • The period of output remaining at valid 0 (before rising to valid 1 eventually) after input that was previously at valid 0 has turned invalid

Note that output remaining at valid 1 means to maintain output voltage value above Voh, while input at valid 1 means to receive input voltage value above Vih. The same applies for valid 0 on both input and output. Revise the lecture on Digital Abstraction if you’re still confused about this concept of valid 0 and 1.

The first two cases are called tc fall, while the latter two cases are called tc rise. The name rise or fall depends on whether the output is about to fall or rise.

The truth table of the nand2 gate is as follows:

a b z
0 0 1
0 1 1
1 0 1
1 1 0

Therefore the computation of tc fall and tc rise for nand2 gate is:

\[\begin{aligned} t_{c_{FALL}} &= \text{time elapsed from when input > Vil to when output < Voh}\\ t_{c_{RISE}} &= \text{time elapsed from when input < Vih to when output > Vol}\\ t_{cd} &= \min(t_{c_{RISE}}, t_{c_{FALL}}) \end{aligned}\]

tc fall is computed based on the third row of the nand2 truth table. We first set the input at valid 0, so we have the output at valid 1. Then, we shall increase the input value to eventually no longer be valid 0 (> Vil) and compute the period of time where the output still remains at valid 1 (before eventually falling). The same logic applies for tc rise.

The computation of tc fall and tc rise is not the same for all gates. For instance, the computation for the two values for a buffer is:

\[\begin{aligned} t_{c_{FALL}} &= \text{time elapsed from when input < Vih to when output < Voh}\\ t_{c_{RISE}} &= \text{time elapsed from when input > Vil to when output > Vol}\\ t_{cd} &= \min(t_{c_{RISE}}, t_{c_{FALL}}) \end{aligned}\]

Pause and ensure you understand how the formulas above are derived.

Similarly, the propagation delay is the period of output invalidity after the inputs have become valid.

That means there are four scenarios, depending on the combination of input and output values:

  • The period of output turning to valid 0 (from being in valid 1 previously) after the input has become a valid 1
  • The period of output turning to valid 0 (from being in valid 1 previously) after the input has become a valid 0
  • The period of output turning to valid 1 (from being in valid 0 previously) after the input has become a valid 1
  • The period of output turning to valid 1 (from being in valid 0 previously) after the input has become a valid 0

The first two cases are called tp fall, while the latter two cases are called tp rise.

Therefore the computation of tp fall and tp rise for nand2 gate is:

\[\begin{aligned} t_{p_{FALL}} &= \text{time elapsed from when input }\geq \text{Vih to when output} \leq \text{ Vol}\\ t_{p_{RISE}} &= \text{time elapsed from when input }\leq \text{Vil to when output} \geq \text{ Voh}\\ t_{pd} &= \max(t_{p_{RISE}}, t_{p_{FALL}}) \end{aligned}\]

Following standard practice, we’ll choose the logic thresholds as follows:

Vol = 10% of power supply voltage = .3V Vil = 20% of power supply voltage = .6V Vih = 80% of power supply voltage = 2.6V Voh = 90% of power supply voltage = 3V

Review the lecture on CMOS Technology to refresh your understanding on propagation delay and contamination delay. This is **VERY** important especially for Week 3 materials.


Generating test signal

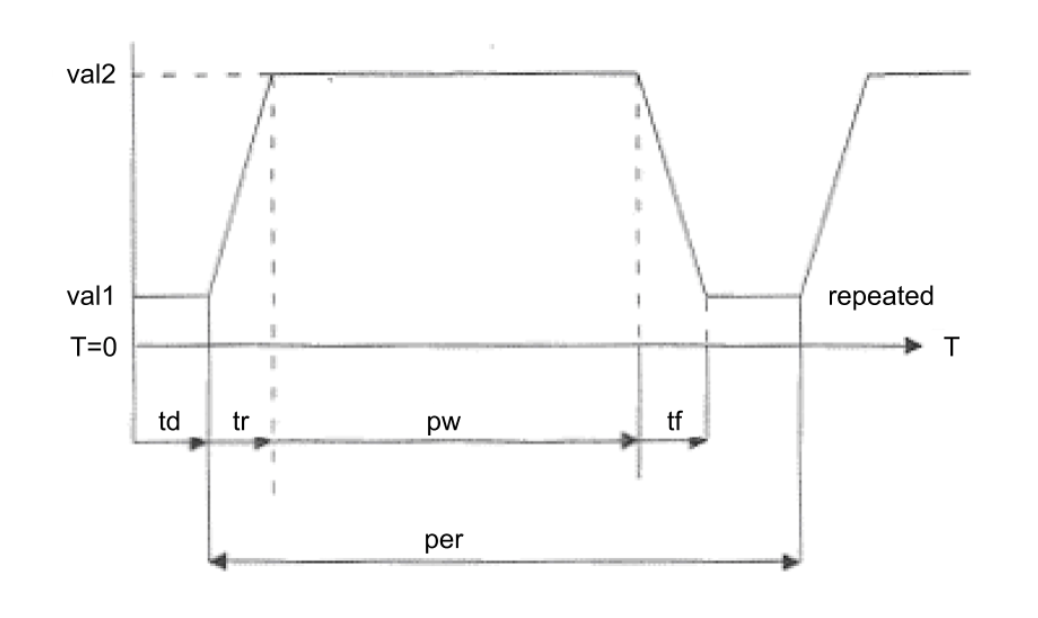
The final thing that we have to prepare to plot a VTC is to generate a test signal. You can use a voltage source with either a pulse or piecewise linear waveform to generate test signals for your circuit. Here’s how to enter them in your netlist:

1

Vid output 0 pulse(val1 val2 td tr tf pw per)

This statement produces a periodic waveform with the following shape:

Task E: Measuring tpd and tcd

Replace the netlist fragment from Task C with the following test circuit that will let us measure various delays:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

* test jig for measuring tcd and tpd
Xdriver vin nin inv
Xtest vdd nin nout nand2
Cload nout 0 .02pf
Vin vin 0 pulse(3.3,0,5ns,.1ns,.1ns,4.8ns)

Vol vol 0 0.3v   // make measurements easier!
Vil vil 0 0.6v
Vih vih 0 2.6v
Voh voh 0 3.0v

.tran 15ns
.plot vin
.plot nin nout vol vil vih voh

Note: make these measurements using your “improved” nand2 gate from Task C that has the centered VTC, i.e., with the updated widths for the PFETs.

  • We use an inverter (inv) to drive the nand2 input since we would normally expect the test gate to be driven by the output of another gate (there are some subtle timing effects that we’ll miss if we drive the input directly with a voltage source).

  • Run the simulation with the “device-level simulation” button and measure the contamination and propagation delays for both the rising and falling output transitions. You will meet such waveforms:

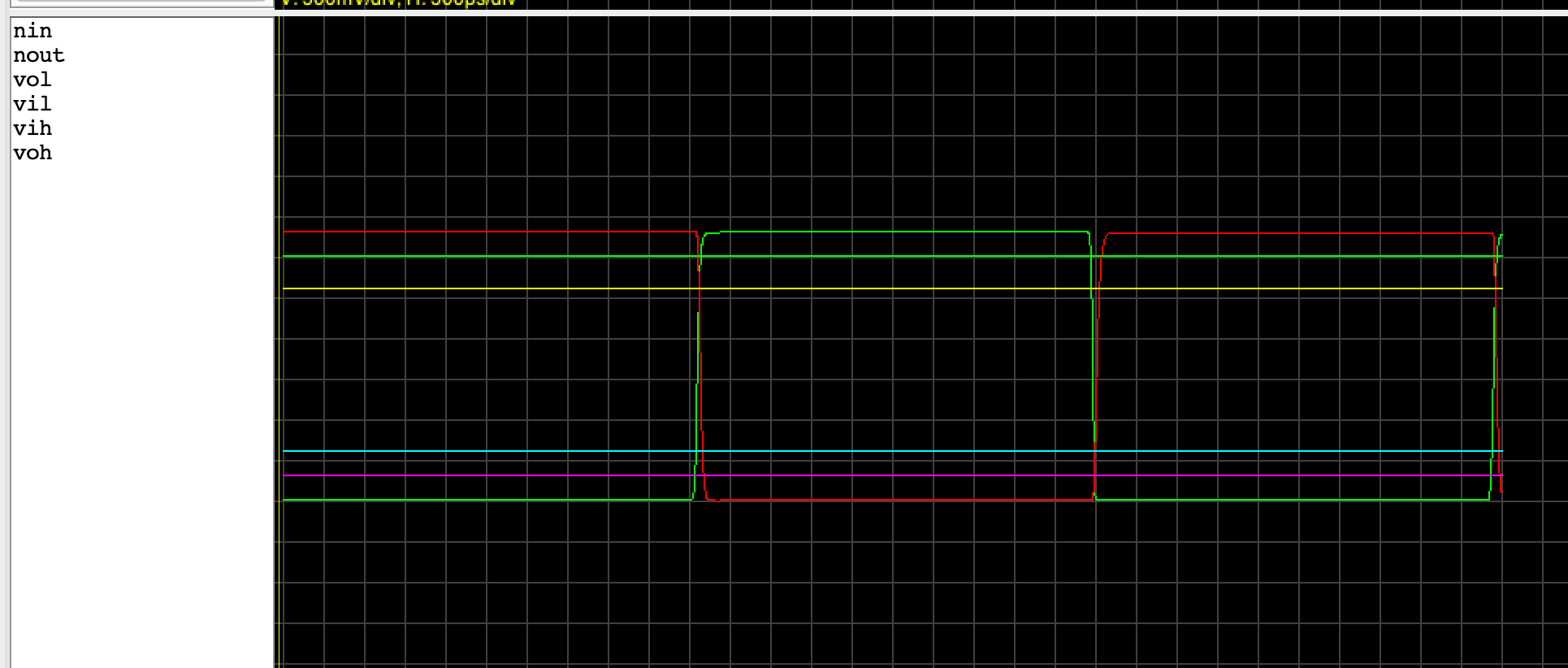
  • You will need to zoom in on the transitions in order to make an accurate measurement.
  • Combine as described above to produce estimates for tc and tp.
**Record** down the contamination tcd and propagation tpd delays for both the rising and falling output transitions. You will need this information for Checkoff 5. Please zoom in at least 4-5 times before doing this to get a clearer picture of the signals.


Task F: Measuring tpd and tcd in 100°C

We always want our computer and electronic circuits operate reliably over a wide range of environmental conditions. It is not a secret that CPUs get real hot doing intense work.

For instance, that’s why we spend big bucks on that RGB-lighted cooling system on our gaming desktops.

We can have JSim simulate our test circuit at a different temperature by adding a .temp control statement to the netlist. Normally JSim simulates the circuit at room temperature (25°C), but we can simulate the circuit at, say, 100°C by adding the following to our netlist:

1

.temp 100

For many consumer products, designs are tested in the range of 0°C to 100°C. Repeat your measurements of Task E at 100°C and report your findings. Recompute your estimates for tC and tP indicating which measurement(s) determined your final choice for the two delays.

**Record** down your findings. You will need this information for Checkoff 6 and 7. Please zoom in at least 4-5 times before doing this to get a clearer picture of the signals.


Based on your experiment, if a 2019 Intel Core i9 processor is rated to run correctly at 2.3 GHz at 100°C, how many % more can you clock it and still have it run correctly at room temperature (assuming tpd is the parameter that determines “correct” computer behavior)?

This is why you can usually get away with overclocking your CPU—it’s been rated for operation under much more severe environmental conditions than you’re probably running it at!

Task G: CMOS Logic Gate Design

As the final part of this lab, your mission is to create and test a CMOS circuitry that implements the function F(A,B,C) = C + A·B using NFETs and PFETs. The truth table for F is shown below:

A B C F(A,B,C)
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1


**Write** your answer in the space provided under inside `lab1_submit.jsim`.


  • Open lab1_submit.jsim and write your answer there:
    • There should be three parts to your answer
      • The pullup circuitry
      • The pulldown circuitry
      • The inverter at the drain of not F CMOS circuitry to produce back F

  • Run it on jsim using the FAST TRANSIENT ANALYSIS button:

  • You will need to understand the output plot, and the meaning of each line of instruction in the answer to be able to excel in the Lab Quiz.
  • Click on the green tick button on the right hand corner of the plot window. A message as such should appear, which means that all values produced by your circuit is as expected:

nominal.jsim and lab1checkoff.jsim contains the necessary circuitry to generate the appropriate input waveforms to test your circuit. It includes a .tran statement to run the simulation for the appropriate length of time and a few .plot statements which will display the input and output waveforms for your circuit.

The solution should contain NO more than 8 MOSFETs. Remember that only NFETs should be used in pulldown circuits and only PFETs should be in pullup circuits. Using six MOSFETs, we implement the complement of F as one large CMOS (complementary MOS) gate and then use the remaining two MOSFETs to invert the output of your large gate.

Refer to the lecture on CMOS Technology to understand how you can construct the circuit using complementary MOSFETs.