50.002 Computation Structures Computation Structures

50.002 Computation Structures
Information Systems Technology and Design
Singapore University of Technology and Design

Problem Set 4

This page contains all practice questions that constitutes the topics learned in Week 4: Turing Machine and Designing an Instruction Set.

Each topic’s questions are grouped into three categories: basic, intermediate, and challenging. You are recommended to do all basic problem set before advancing further.

Note that the amount of practice problems in this week’s set is smaller than usual because the topics learned this week is mainly to set-up the knowledge required for the following week. Please head to PS5 for more practice problem.

Turing Machine

Ben’s Turing Machine (Basic)

Ben Bitdiddle’s proposed Ph.D. thesis involves writing a program to compute a function $f(x)$ on a Cray supercomputer. Ben’s advisor points out that $f$ cannot be computed on any Turing machine. Should Ben care? Why?

Show Answer

Church's thesis says that if the function can't be computed on any Turing machine, then it can't be computed on any physically realizable machine that we know of. So Ben is out of luck... a Cray supercomputer isn't "super" in that sense.


Discouraged by your answer to the last question, Ben has turned his attention to an alternative thesis topic. He now proposes to invent the universal FSM, which will be to FSMs what a universal Turing machine is to Turing machines. Ben’s idea is to build an FSM that can fed a sequence of inputs describing any other FSM and the inputs to that FSM. The universal FSM would then emulate the behavior of the described FSM on the specified inputs. Is Ben’s idea workable Why or why not?

Show Answer

Unfortunately, the Universal FSM will have some fixed number (N) of states built into its design. So it won't have enough states to emulate machines with more than N states. Ben's idea isn't workable, and there's no such thing as "Universal FSM" as he proposed.


FSM in TM (Intermediate)

We encode the state of a Turing machine into 2 bits, the value that is read (input) from and written (output) onto the infinite tape into 2 bits, and the output move on the tape (left or right) into 1 bit. How many different finite state machines are there to control such a Turing machine?

Show Answer

From the explanation above, we have:

  • $s$ = 2
  • $i$ = 2
  • $o$ = 3
We can enumerate $2^{(s+o)2^{s+i}}$ FSM, and hence the answer to this question is $2^{80}$


Running a Turing Machine (Basic)

You are given a Turing machine (TM) with three states (S0, S1, S2) and a HALT state and the following state transition diagram and state table. The TM operates by reading and then moving either left (“L”) or right (“R”) on an infinite tape. Note that the question defined it as we move the machine here not the tape.

The tape is used to encode a binary number with three symbols, “0”, “1” and “_”, where “_” is used to signal the beginning and end of the number. For instance, the binary number “1011” is represented on the tape as _,1,0,1,1,_ (most significant bit on the left).

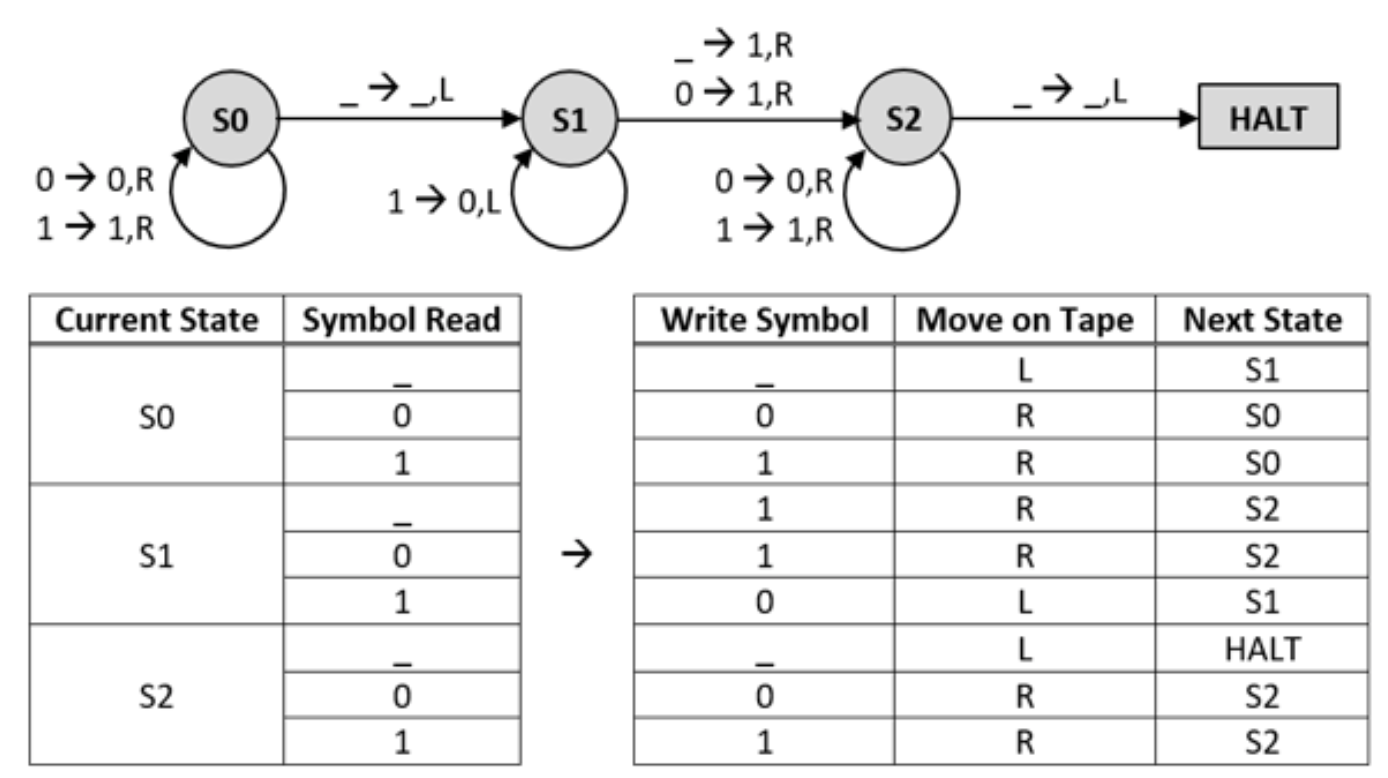
If the tape is in the initial configuration _,1,0,1,1,_:

  • and the Turing machine starts in state S0,
  • reading at the tape position of the 0,

…what is the state transition sequence that the machine is going to execute (including the start state S0) until it meets a HALT?

Show Answer

Answering this is none other than executing the Turing Machine with the given tape _,1,0,1,1,_ and initial state `S0`, with the machine reading the tape at the 0.

The sequences of the states until HALT is met is: S0, S0, S0, S0, S1, S1, S1, S2, S2, S2, HALT


What is the final configuration of the tape after the TM has halted and what does the TM do?

Show Answer

The final tape configuration is: _,1,1,0,0,_ It is obvious that the TM adds 1 to the input number.


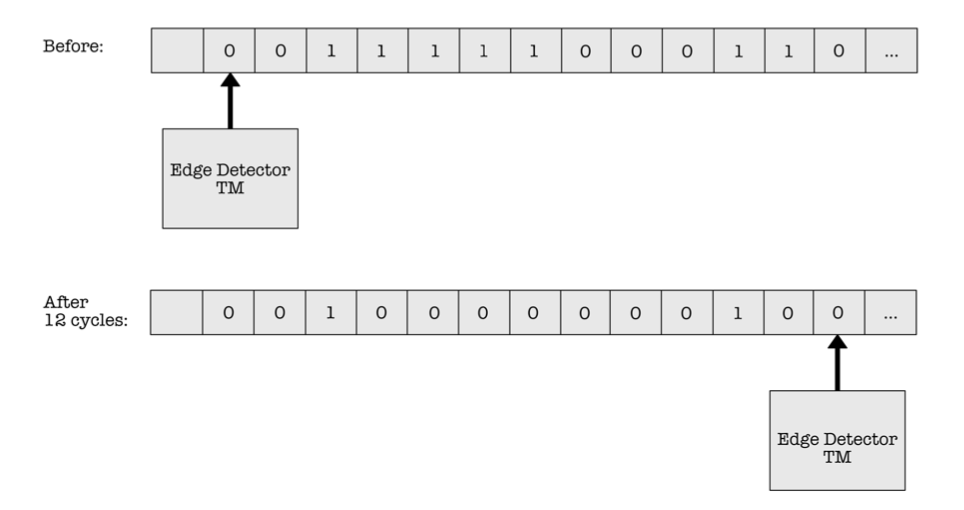
Edge Detector Machine (Intermediate)

The figure below shows a particular tape state before and after a Turing Machine that does edge detection is executed for 12 steps (12 clock cycles).

Indicate which of the following Turing Machine specification [A], [B], [C], [D], [E] shown below is/are able to produce the “after” tape state *in exactly 12 cycles.

  • Specification 1: \(\begin{matrix} S_i & \text{Input} & S_{i+1} & \text{Output} & \text{Move Tape}\\ \hline S_0 & 0 & S_0 & 0 & L\\ S_0 & 1 & S_1 & 1 & L\\ S_1 & 0 & S_0 & 0 & L\\ S_1 & 1 & S_2 & 0 & L\\ S_2 & 0 & S_0 & 0 & L\\ S_2 & 1 & S_2 & 0 & L\\ \hline \end{matrix}\)

  • Specification 2: \(\begin{matrix} S_i & \text{Input} & S_{i+1} & \text{Output} & \text{Move Tape}\\ \hline S_0 & 0 & S_0 & 0 & L\\ S_0 & 1 & S_1 & 1 & L\\ S_1 & 0 & S_0 & 0 & L\\ S_1 & 1 & S_1 & 1 & L\\ \hline \end{matrix}\)

  • Specification 3: \(\begin{matrix} S_i & \text{Input} & S_{i+1} & \text{Output} & \text{Move Tape}\\ \hline S_0 & 0 & S_0 & 0 & L\\ S_0 & 1 & S_1 & 1 & L\\ S_1 & 0 & S_0 & 0 & L\\ S_1 & 1 & S_1 & 0 & L\\ \hline \end{matrix}\)

  • Specification 4: \(\begin{matrix} S_i & \text{Input} & S_{i+1} & \text{Output} & \text{Move Tape}\\ \hline S_0 & 0 & S_0 & 0 & L\\ S_0 & 1 & S_1 & 1 & L\\ S_1 & 0 & S_0 & 0 & L\\ S_1 & 1 & S_2 & 1 & L\\ S_2 & 0 & S_0 & 0 & L\\ S_2 & 1 & S_2 & 1 & L\\ \hline \end{matrix}\)

  • Specification 5: \(\begin{matrix} S_i & \text{Input} & S_{i+1} & \text{Output} & \text{Move Tape}\\ \hline S_0 & 0 & S_0 & 0 & L\\ S_0 & 1 & S_1 & 1 & R\\ S_1 & 0 & S_0 & 0 & L\\ S_1 & 1 & S_2 & 0 & R\\ S_2 & 0 & S_0 & 0 & L\\ S_2 & 1 & S_2 & 0 & R\\ \hline \end{matrix}\)

Show Answer

Specification 1 and Specification 3 produces the same output tape as shown above, given the initial tape content and the Turing Machine's start state (and location). We can run the machine five times with each specifications to obtain the answer, but the faster way is to observe them based on the functionality:

  • To detect an edge, there's no need to "re-read" previous input. Therefore Specification 5 is definitely wrong (we only need to move the tape in one direction).
  • We only output 1 once on the occurence of an edge, so the specification shall not output too many 1s. You can then start to suspect whether Specification 2 and 4 are true, and quickly eliminate them from the pool of possible answers.


Designing an Instruction Set

CPU Trivia (Basic)

  1. How much memory can a 32-bit von Neumann machine have? Explain your answer.

    Show Answer

    $2^{32}$ bytes because each address is also 32 bits long in a 32-bit von Neumann machine.


  2. Can a CPU have as many registers as possible, in theory?

    Show Answer

    No. Addresses for each register involved in the instruction must be encoded within the instruction, i.e: 5 bits for 32 registers. An instruction is 32 bits long for $\beta$ architecture, so having too many registers will make encoding infeasible.


  3. In Theory, which machine is least powerful but sufficient to compute each of the following functions? Choose for the four following possible choices ranked by its level of “powerfullness”:

    • Turing Machine (most powerful)
    • FSM
    • Combinational Logic (least powerful)
    • Uncomputable

    The functions in question are:

    • Function 1: A processor that executes Beta instruction set

    • Function 2: A device which takes as input the digits of a binary integer from left to right, and output 1 if the number entered so far is divisible by 6, and 0 otherwise.

    • Function 3: A device that takes a sequence of binary digits, one each milisecond clock period, and output 1 if the sequence so far contains more 1s than 0s.

    • Function 4: A device that takes as input an integer n between 0 and 20, and outputs the closing price of Apple Stock on the n$^{th}$ trading day of year 2019 (to the nearest whole dollar)

    Show Answer

    Function 1: FSM
    Function 2: FSM
    Function 3: Turing Machine
    Function 4: Combinational Logic


Memory Addressing (Basic)

  1. You are given that the 32-bit word at memory address 0 has a binary form of 
     0000 0100 0000 0011 0000 0010 0000 0001

    What is the value of the byte stored in address 0, 1, 2 and 3, respectively? What are the hexadecimal forms of the bytes?

    Show Answer

    1, 2, 3, and 4 are stored at address 0, 1, 2, 3 respectively. The hex form is the word: 0x04 03 02 01.


  2. How many bits of addresses are required at minimum to address the following chunk of data, assuming that they are byte addressable?

     0000 0100 0000 0011 0000 0010 0000 0001
 1111 1111 0000 0000 1111 1111 0000 0000
 1010 1010 0011 1100 0101 0011 0011 0000 
 0000 0011 0010 1100 0101 1100 1100 0001
 0000 0000 0000 0000 0000 1100 1100 0001
    Show Answer

    There are 20 bytes in the data above. We need at least $\lceil\log_2(20)\rceil$= 5 bits for addressing.