50.002 Computation Structures Computation Structures

50.002 Computation Structures
Information Systems Technology and Design
Singapore University of Technology and Design

Problem Set 1

This page contains all practice questions that constitutes the topics learned in Week 1: Basics of Information and The Digital Abstraction.

Each topic’s questions are grouped into three categories: basic, intermediate, and challenging. You are recommended to do all basic problem set before advancing further.

Basics of Information

You can refer to the notes here if you need to revise.

Warm Up (Basic)

Suppose that you are to guess the value of a 16-bit number: 0x$Z_1Z_2Z_3Z_4$ You are told that the value of $Z_1$ is B. Thus you have been given [N] bits of information. What is the value of [N]?

Show Answer

Obviously $Z_x$ represents **4 bits** since these are in hexadecimal number system (indicated with the prefix 0x.)

We are literally told that the first hex digit is $B = 1011$. Hence we are given 4 bits of information. There are still other 12 bits which values we do not know.


Keyboard Presses (Basic)

(a). Bob used an enhanced keyboard that was made up of 101 keys. He told Alice that he pressed one of the letter keys. How much information did Bob give to Alice? Hint: There are 26 letters in an alphabet.

Show Answer

Initially, there's $101$ choices. The information that Bob gave Alice narrows down the choices into 26. The information given is therefore $\log_2(101) - \log_2(26) = 1.958$.


(b). Bob used an enhanced keyboard that was made up of 101 keys. He told Alice that he pressed two of the letter keys consecutively. Bob did not mention whether the two keys are the same or not. How much information did Bob give to Alice? Hint: There are 26 letters in an alphabet.

Show Answer

Initially, there are $101*101$ choices.

Pressing two letter keys consecutively (might be repeated) narrows down the choices onto $26_*26$.

Hence the information given is $\log_2(101^2) - \log_2(26^2) = 3.916$.


ISTD Prize (Intermediate)

Your cohort in ISTD contains 100 students:

  • 51 of whom are male and 49 are female.
  • There are 31 male students who are above 19 years old.
  • On the other hand, there are 19 female students who are above 19 years old.
  • There are one male student and three female students who like to have a final exam.

    You can assume that students either like or hate a final exam and no indifference.

  • Two students like exam and is above 19 years old.

Now someone in your class won “the first to join ISTD” prize. Answer the following questions:

(a.) If you are told the student ID of this winner, how much information did you receive in bits?

Show Answer

If we are given the student ID, we effectively know who the winner is. We instantly narrow down our pool of winner candidates from 100 students into just 1 student, hence the bits of information given is $\log_2(100)$.


(b.) If you are told the student ID of the last 33 students who joined ISTD, how much information did you receive in bits?

Show Answer

If we know the last 33 students who joined ISTD, we know that these students cannot be the winner. Hence our pool of candidates are narrowed down into 67 students. We are then given $\log_2(100) - \log_2(67)$ bits of information.


(c.) If you are told that the student who won the “first to join ISTD prize” is a male, how much information did you receive in bits?

Show Answer

Similarly, there are 51 males in ISTD. Hence, we are given $\log_2(100) - \log_2(51)$ bits of information.


(d.) If you are told that the student who won the “first to join ISTD prize” is above 19 years old instead, how much information did you receive in bits?

Show Answer

Our candidates are narrowed down into $31 + 19 = 50$ students instead since there are 50 students who are above 19 years old. The amount of information given is $\log_2(100) - \log_2(50)$ bits.


(e.) If you are told that the student who won the “first to join ISTD prize” hated a final exam and is below 19 years old, how much information did you receive in bits?

Show Answer

There are $51-31 = 20$ male students that are below 19 years old. There are also 30 female students that are below 19 years old. Since there are only 4 people who like exam, and 2 of them are above 19 years old, there's only 2 students who are below 19 years old and like exam as well.
</br> Hence our candidates are further narrowed into 48 students after knowing that the person does not like exam. This gives us $\log_2(100 ) - \log_2(48)$ bits of information.


Deck of Cards (Intermediate)

(a.) Someone picks a name out of a hat known to contain the names of 5 women and 3 men, and tells you a man has been selected. How much information have they given you about the selection?

Show Answer

Originally, we have 8 options: $M=8$. The option is narrowed down into 3, hence $N = 3$, we have: $$\begin{aligned} I = \log_2 \left(\frac{1}{N/M}\right) = \log_2 \left(\frac{1}{3/8}\right) \text{ bits of information}. \end{aligned}$$


(b.) You’re given a standard deck of 52 playing cards that you start to turn face up, card by card. So far as you know, they’re in completely random order. How many new bits of information do you get when the first card is flipped over? The fifth card? The last card?

Show Answer

The first card has $\log_2 52$ bits of information. The fifth card has $\log_2 48$ bits of information. The last card has 0 bits of information.


(c.) X is an unknown N-bit binary number $(N>3)$. You are told that the first three bits of X are 011. How many bits of information have you been given?

Show Answer

3 bits of information have been given.


(d.). X is an unknown 8-bit binary number. You are given another 8-bit binary number, Y, and told that the Hamming distance (number of different bits) between X and Y is one. How many bits of information about X have you been given when Y is presented to you?

Show Answer

Originally, we have 8 unknown bits, that is $N=2^8$ choices. We can obtain X by flipping any one bit in Y. Since there are 8 bits, there are 8 possibilities for X by flipping each bit in Y. Therefore after given Y, we are down to $M=8$ choices, each having 1 bit that's different for X. We can say that we have been given, $$\begin{aligned} I = \log_2 \left(\frac{1}{M/N}\right) = \log_2 \left(\frac{1}{8/2^8}\right) = 5 \text{ bits of information}. \end{aligned}$$


Measuring Information (Basic)

After spending the afternoon in the dentist’s chair, Ben has invented a new language called DDS made up entirely of vowels (the only sounds he could make with someone’s hand in his mouth). The DDS alphabet consists of the five letters: A, E, I, U, O, which occur with the following probabilities,

Letter Probability
A P(A) = 0.15
E P(E) = 0.4
I P(I) = 0.15
O P(O) = 0.15
U P(U) = 0.15

If you’re told that the first letter of the message is “A”, give an expression for the number of bits of information you have received.

Show Answer

Recall that the information received is inversely proportional to the probability of that choice occurring, and we take $\log_2$ of the probability of that choice occurring to quantify the information in terms of bits. Hence the expression is, $$I = \log_2 \frac{1}{p(A)}$$


Modular arithmetic and 2’s complement representation (Basic)

Most computers choose a particular word length (measured in bits) for representing integers and provide hardware that performs various arithmetic operations on word-size operands. The current generation of processors have word lengths of 32 bits; restricting the size of the operands and the result to a single word means that the arithmetic operations are actually performing arithmetic modulo $2^{32}$.

Almost all computers use a 2’s complement representation for integers since the 2’s complement addition operation is the same for both positive and negative numbers. In 2’s complement notation, one negates a number by forming the 1’s complement (i.e: for each bit, changing 0 to a 1 and vice versa) representation of the number and then adding 1. By convention, we write 2’s complement integers with the most-significant bit (MSB) on the left and the least-significant bit (LSB) on the right. Also, by convention, if the MSB is 1, the number is negative, otherwise it’s non-negative.

(a.) How many different values can be encoded in a 32-bit word?

Show Answer

$2^{32}$.


(b.) Please use a 32-bit 2’s complement representation (signed bits) to answer the following questions. What are the representations for:

  1. Zero
  2. The most positive integer that can be represented
  3. The most negative integer that can be represented
Show Answer

  1. 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
  2. 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
  3. 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0


(c.) What are the decimal values for the most positive and the most negative number that can be represented by this signed 32-bit machine?

Show Answer

The most positive value in decimal: 2147483647. The most negative value in decimal: -2147483648


(d.) Since writing a string of 32 bits gets tedious, it’s often convenient to use hexadecimal representation where a single digit in the range of 0-9 or A-F is used to represent groups of 4 bits. Give the 8-digit hexadecimal equivalent of the following decimal and binary numbers:

  1. $37_{10}$
  2. $-32768_{10}$
  3. 1101 1110 1010 1101 1011 1110 1110 1111
Show Answer

  1. 0x 0000 0025
  2. We begin by converting $32768$ (positive) number to Hex: 0x 0000 8000. Then we take the 1's complement. Note: transform the hex to binary first and flip the bits, then transform back to hex: 0x FFFF 7FFF, and finally +1 : 0x FFFF 8000.
  3. 0x DEAD BEEF


(e). Calculate the following using 6-bit 2’s complement arithmetic (which is just a fancy way of saying to do ordinary addition in base 2, keeping only 6 bits of your answer). Show your work using binary notation. Remember that subtraction can be performed by negating the second operand and then adding to the first operand.

  1. 13 + 10
  2. 15 - 18
  3. 27 - 6
Show Answer

  1. 001101 + 001010 = 010111
  2. 18 is 010010. -18 is 101110. Hence, 001111 + 101110 = 111101.
  3. 011011 + 111010 = 010101


Dice Throwing Game (Intermediate)

A group of five friends are playing a game that requires them to generate random numbers using 10 fair dice in the beginning before proceeding with the game. They each will throw the 10 dice and sum up all the outcomes of the dice to get the random number. Answer the following questions:

(a.) How many bits at the minimum (so round up your answer to the nearest integer) are required to encode all distinct numeric outcomes of 10?

Show Answer

The maximum number you can get from summing 10 dice throws is 60, and the minimum is 10. Therefore you have 51 possible combinations, which require $\log_2(51)$ bits to represent. Rounding up, this results in 6 bits.


(b.) Someone in the group suggests that they can just use a die and throw it 10 times to get the random number required for the game. This way, they don’t have to deal with carrying so many dice. The game began and then he proceeded with throwing the die. His first 3 throws are: 1, 3, and 4. How many bits of information has been given so far? Give your answer in 3 decimal places.

Show Answer

Each dice throw can result in any number between 1 to 6, which requires $\log_2(6)$ bits to encode. Three dice throws give you $3 * \log_2(6) = 7.755$ bits.


(c.) After throwing the die 9 times in total, how many new bits of information did he get from making the last (the 10th) throw? Give your answer in 3 decimal places.

Show Answer

With the same idea as the previous part, the last dice throws solve the mystery on whether we will get number 1, 2, 3, 4, 5, or 6. Hence we are given $\log_2(6)=2.585$ bits from the last throw.

Note that this is significantly different from the bits of information that has been given to us so far. The nine dice throws have given us $9*log2(6)$ bits of information. The last nice throws give us another $\log_2(6)$ bits of information. Please be careful with the wording.


(d.) Finally, he found that the number he got in total from all 10 throws is 53. Express this number in 3-digit hex, formatted as 0xZZZ where Z is your answer.

Show Answer

0x035


Another Base Conversion (Basic)

Consider an 8-bit signed number systems. Do the following base conversion, and indicate with a 0b prefix for binary systems and 0x prefix for hexadecimal systems. Octal and decimal systems do not have prefixes.

  1. 76 (decimal) to binary
  2. 0b10000001 (binary) to decimal
  3. 0b10011101 (binary) to hexadecimal
  4. 0xBF (hexadecimal) to binary
  5. 0xC6 (hexadecimal) to octal
Show Answer

  1. 0b01001100
  2. -127
  3. 0x9D
  4. 0b10111111
  5. 306


Representing -32 on different number systems (Basic)

Which of the following signed numbers is the representation of number -32 for either an 8-bit or 16-bit system? Note: the answer must be either 8-bit or 16-bit long.

  1. 0b1010 0000
  2. 0b1110 0000
  3. 0b0001 0000
  4. 0xE0
  5. 0x80E0
  6. 0xFFE0
  7. 0x10E0
  8. 0x800000E0
  9. 0xFFFFFFE0
Show Answer

(2), (4), (6)


Proof of 2’s Complement (Challenging)

At first blush, “Complement and add 1” doesn’t seem like an obvious way to negate a two’s complement number. By manipulating the expression $A + (-A) = 0$, show that “complement and add 1” does produce correct representation for the negative of a two’s complement number.

Hint: express 0 as (-1 + 1) and rearrange the terms to get -A on one side and ZZZ+1 on the other and then think about how the expression ZZZ is related to A using only logical operations (AND, OR, NOT).

Also, see how binary subtraction ‘borrow’ method works here if you dont know how it works.

Show Answer

Let: $$\begin{aligned} (-A) &= -A - 1 + 1\\ &= (-1 - A) + 1 \end{aligned}$$ In this case, ZZZ is $(-1-A)$. Now, let's say we have 8 bit number. We can represent -1 using all 1's : 1111 1111. Then, lets represent A arbitrarily as a7 a6 a5 a4 a3 a2 a1 a0, where $a_i$ can be 0 or 1.

Subtracting -1 with A will flip the bits of A, such that if $a_i = 0$, then $1 - a_i = 1$, and if $a_i = 1$ then $1- a_i = 0$. Hence, we can rewrite the above into, $$\begin{aligned} (-A) &= \text{bitwise NOT } A + 1 \end{aligned}$$ which is exactly the two complement's steps.


The Digital Abstraction

You can refer to the notes here if you need to revise.

VTC Plot (Basic)

The behavior of a 1-input 1-output device is measured by hooking a voltage source to its input and measuring the voltage at the output for several different input voltages, resulting in the following VTC plot,

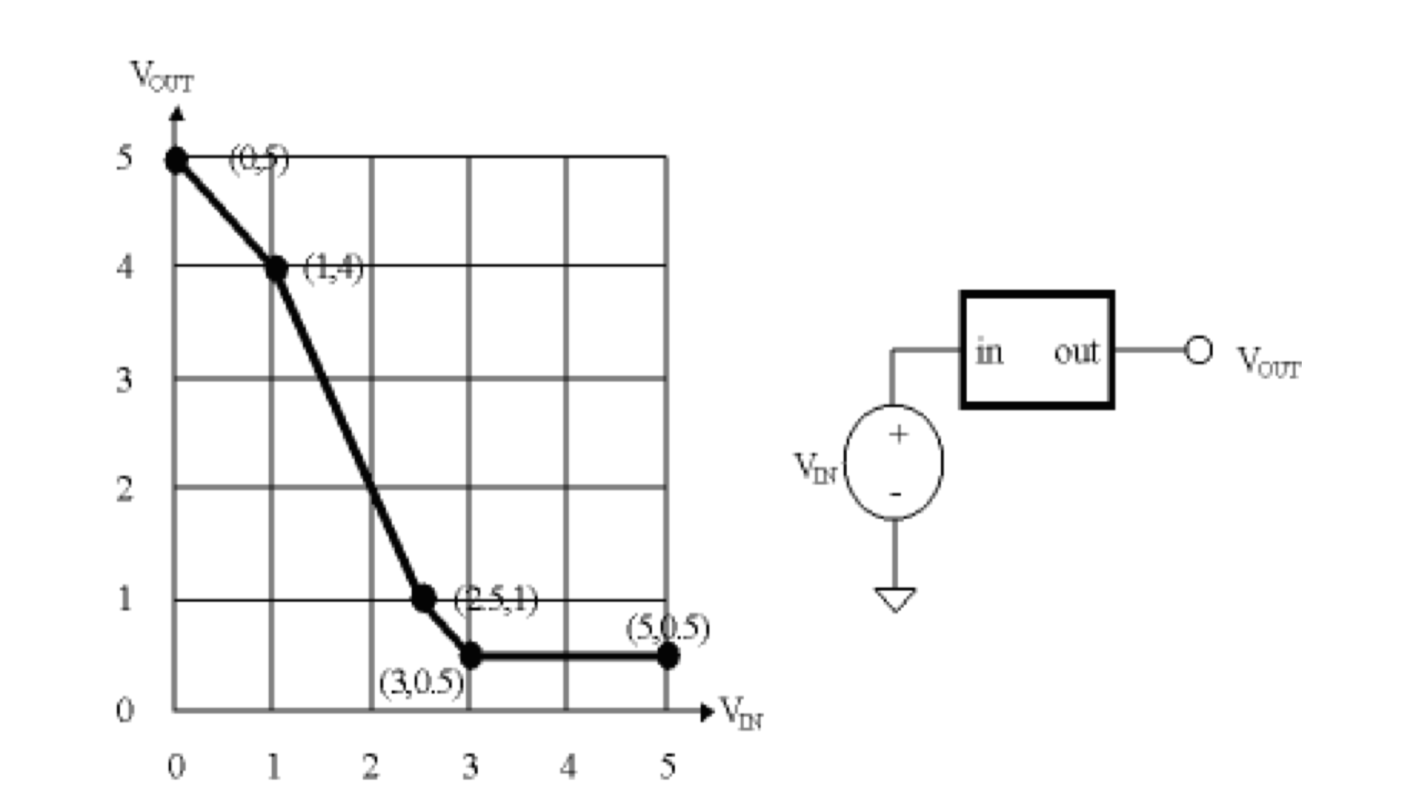
We’re interested in whether this device can serve as a legal combinational device that obeys the static discipline. For this device, obeying the static discipline means that,

\[\begin{aligned} \text{If } V_{IN} \leq V_{IL} \text{ then } V_{OUT} \geq V_{OH}, \text{ and if } V_{IN} \geq V_{IH} \text{ then } V_{OUT} \leq V_{OL} \end{aligned}\]

When answering the questions below, assume that all voltages are constrained to be in the range of 0V to 5V,

  1. Can one choose a $V_{OL}$ of 0V for this device? Explain.
  2. What’s the smallest $V_{OL}$ one can choose and still the device obey the static discipline?
  3. Assuming that we want to have 0.5V noise margins for both “0” and “1” values, what are the appropriate voltage levels for $V_{OL}$, $V_{IL}$, $V_{IH}$, and $V_{OH}$ so that the device obeys the static discipline? Hint: there are many choices. Just choose the one that obeys the static discipline and the NM constraint.
  4. What device is this called?
Show Answer

  1. No. From the plot, it can be seen that $V_{OUT}$ can never reach below 0.5V. If $V_{OL}$ is chosen to be 0V, then the device doesn't satisfy the static discipline anymore.

  2. 0.5V. That is the lowest amount of $V_{OUT}$ that the device can produce.

  3. We can choose $V_{OL} = 0.5V$ from the graph, since the device is capable of producing such low voltage. With NM of 0.5V, that means that $V_{IL} = V_{OL} + 0.5V = 1V$. From the graph, we can also choose $V_{OH} = 4V$, as the part with the highest gain in the middle of the graph can most probably be the forbidden zone. Therefore, $V_{IH} = V_{OH} - 0.5V.= 3.5V$.

  4. This device is an inverter, since a high input produces a low output and vice versa.


Inverter Madness (Intermediate)

(a). The following graph plots the VTC for a device with one input and one output. Can this device be used as a combinational device in logic family with 0.75 noise margins?

Show Answer

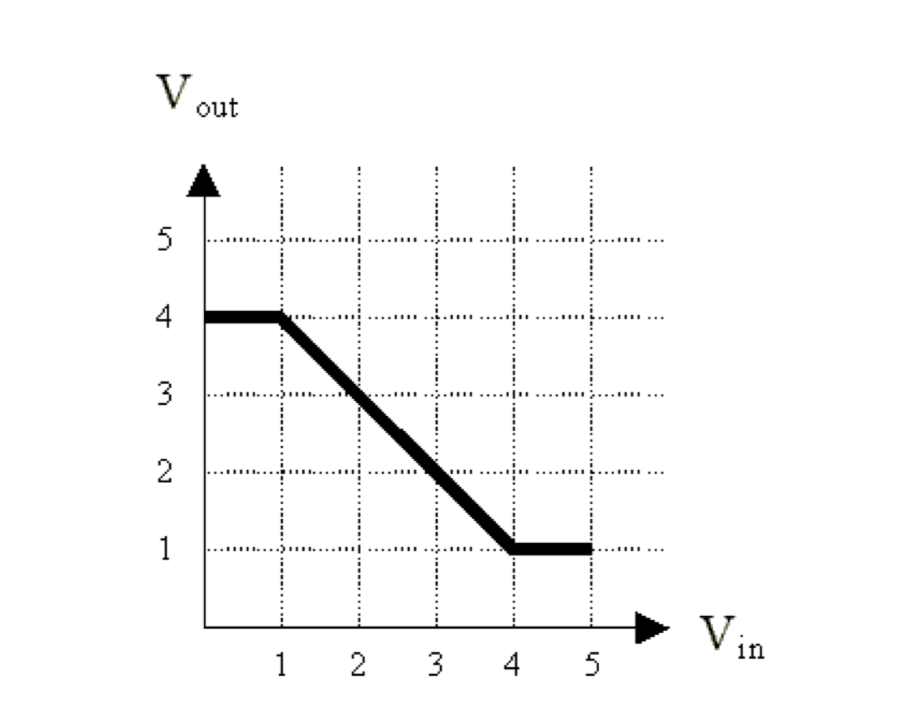
No. This device gain is $\leq1$, hence it cannot be used as a combinational device.


(b). You are designing a new logic family and trying to decide on values of the four parameters: $V_{OL}$, $V_{IL}$, $V_{IH}$, and $V_{OH}$ that lead to non-zero noise margins for various possible inverter designs. Four proposed inverter designs exhibit the VTC shown in the diagrams below. For each design, either specify four suitable values of $V_{OL}$, $V_{IL}$, $V_{IH}$, and $V_{OH}$ or explain why no values can obey the static discipline.

Hint: you may want to start by choosing NM to be 0.5V for ease of computation.

Show Answer

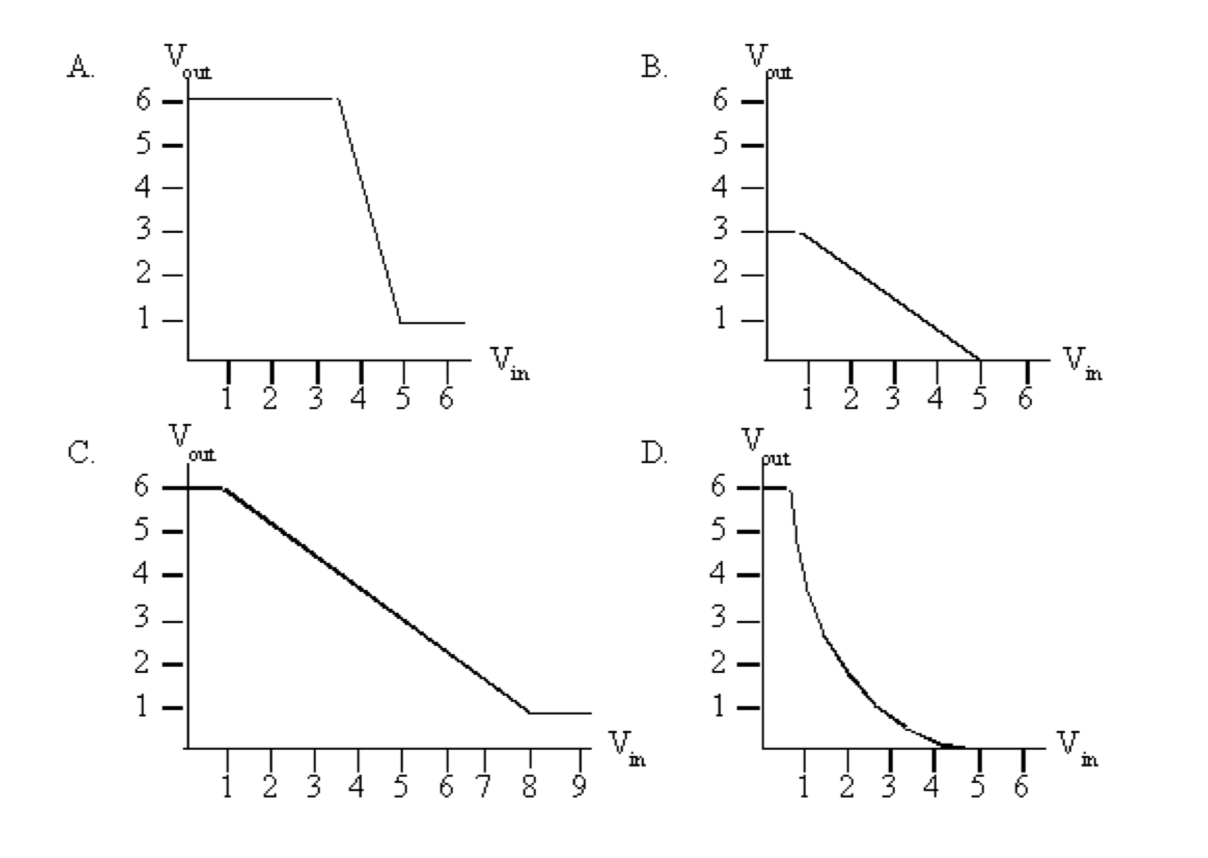
(B) and (C) cannot be used as inverter (combinational device) as its gain is $\leq1$.

For (A), choose NM = 0.5V, then $V_{OL} = 1V$, $V_{IL} = 1.5V$, $V_{IH} = 5V$, and $V_{OH} = 5.5V$.

For (D), choose NM = 0.5V, then $V_{OL} = 0.5V$, $V_{IL} = 1V$, $V_{IH} = 5$, and $V_{OH}= 5.5V$.


Static Discipline (Basic)

(a). Consider a combinational buffer with one input and one output. Suppose we set its input to some voltage $V_{IN}$, wait for the device to reach a steady state, then measure the voltage on its output $V_{OUT}$ and find out $V_{OUT} < V_{OL}$. What can we deduce about the value of $V_{IN}$?

Show Answer

We have a valid low output, but that doesnt mean that we have a valid low input. However we know for sure that input cannot be higher than $V_{IH}$ because static discipline requires the output to be higher than $V_{OH}$ if this is the case for a buffer.

Hence, the only thing we can infer is that$V_{IN} < V_{IH}$ (means input voltage is either a valid low or an invalid value).


(b). Now consider an inverter. Suppose we set its input to some voltage $V_{IN}$, wait for the device to reach a steady state, then measure the voltage on its output $V_{OUT}$, and find $V_{OUT} > V_{OH}$. What can we deduce about the value of $V_{IN}$?

Show Answer

We have a valid high output, but that doesnt mean that we have a valid low input. Static discipline states that given a valid input, the device is always able to give a valid output, but it does not mean that the reverse is true, i.e: invalid input does NOT have to give out invalid output.

However we do know for sure that the input cannot be higher than $V_{IH}$ because static discipline requires the output to be lower than $V_{OL}$ if this is the case for an inverter. Hence, the only thing we can infer is that $V_{IN} < V_{IH}$ (means input voltage is either a valid low or an invalid value).


VTC Analysis (Intermediate)

Take a look at the figure below.

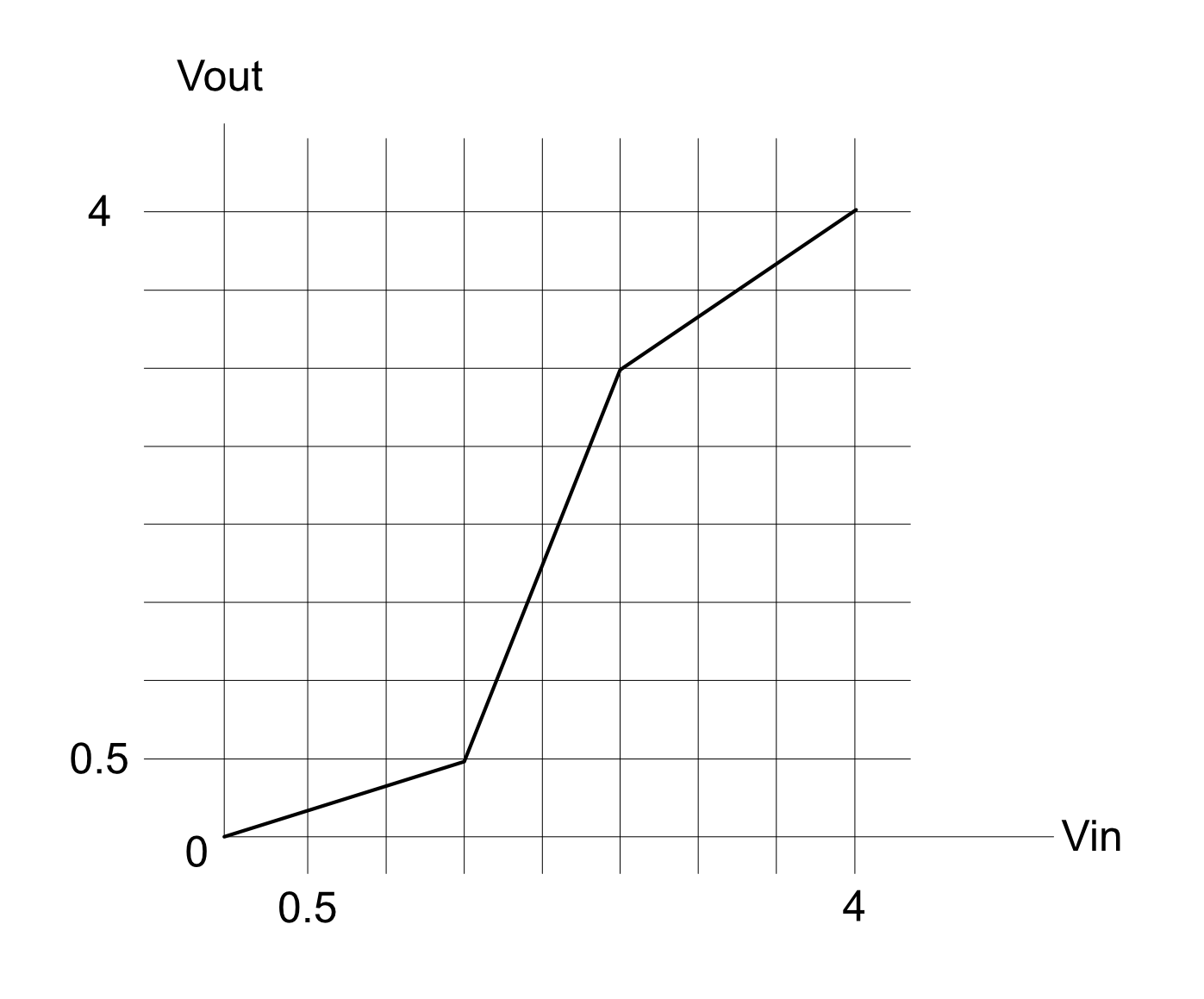
Which of the following specification(s) does not obey the static discipline? Select all that apply.

  1. $V_{IL} = 0.4V, V_{IH} = 3.1V, V_{OL} = 0.2V, V_{OH} = 4.2V$

  2. $V_{IL} = 0.5V, V_{IH} = 3V, V_{OL} = 0.3V, V_{OH} = 4V$

  3. $V_{IL} = 0.2V, V_{IH} = 3V, V_{OL} = 0.4V, V_{OH} = 4.2V$

  4. $V_{IL} = 0.5V, V_{IH} = 4V, V_{OL} = 0V, V_{OH} = 3.5V$

  5. $V_{IL} = 0.5V, V_{IH} = 3.5V, V_{OL} = 0V, V_{OH} = 4V$

Show Answer

None of them obey the static discipline. You may easily check whether the device is able to provide the prescribed $V_{OH}$ given a corresponding $V_{IH}$ in the options, and whether it is able to provide as well the given $V_{OL}$ given a coresponding $V_{IL}$ in the options from tracing the graph.