50.002 Computation Structures Computation Structures

50.002 Computation Structures
Information Systems Technology and Design
Singapore University of Technology and Design

Basics of Information

Overview

In this course, we are going to learn how to build the general-purpose digital device that we call computer these days from the bottom up.

We will start with understanding how we can encode information in terms of voltages, and then how to utilize transistors to synthesize logic. We can use them to create a bigger – more complex programmable system, and eventually with a properly designed instruction set, we can understand how a general purpose programmable machine is made.

In this chapter, we will begin our journey by learning how we can represent and encode information, and then followed by how we can store this information in a tangible form using voltages (next chapter).

Information is defined as knowledge communicated or received concerning a particular fact or circumstance.

It resolves uncertainty.

We can quantify information in electronic devices in terms of bits (binary digits, consisted of simply 1s and 0s). Strings of bits can represent integer values. Therefore we can use them in a way so that our devices can perform (mathematical) computation using this form of quantified information.

Binary Number System

Our computers are electronic devices that can only store informations in terms of electrical signals: high signal and low signal. Therefore we need to work using the binary (base 2) number system and not the decimal number system that we are more familiar with.

How do we represent integers (basic numbers) in binary? Suppose we have binary number:

0 0 1 1 0 1

The above means the integer value: $0 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 13$ in decimal (base 10).

Binary to Decimal conversion is really simple, but takes time to get used to.

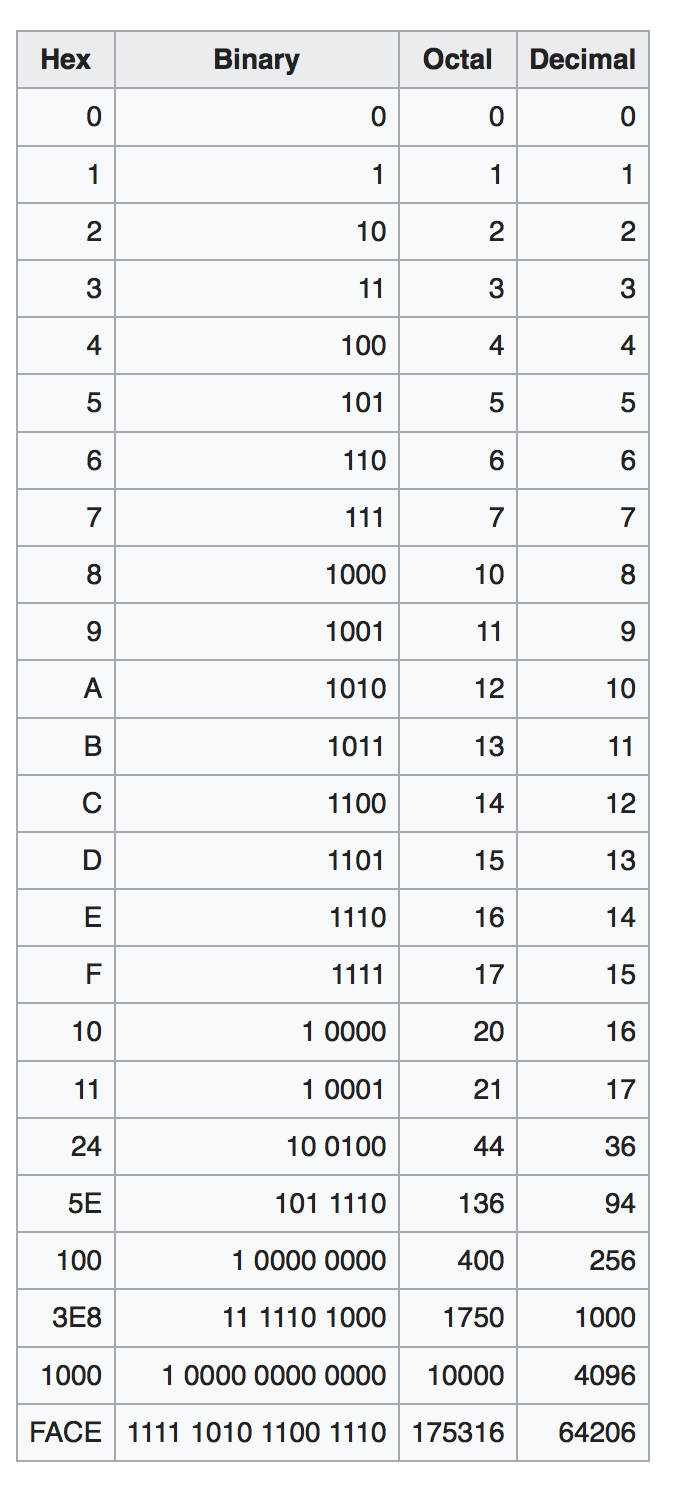
Hex and Octal Number System

What if encoding in binary is too long on paper or text editor? We can use other number systems: encode in octal (base 8) or hex (base 16) to shorten its representation, so that it’s more “human friendly” to write.

See the table below to find out the direct conversion between binary, octal, hex, and decimal.

After some practice, it should be easy to naturally guess the decimal value of any 4-bit number without computing them from scratch.

Note:

  • We typically use the prefix 0x to indicate that a number system is encoded in hex and not decimal.
  • If we encode a number in binary, we can use the prefix 0b or not at all (because it is pretty obvious since a string of numbers only contain 0s and 1s).
  • Numbers encoded in oct will have the suffix $_8$.

The examples below should provide a straightforward hints on how to convert between the number systems.

Example 1:

  1. Binary : 101 101 101 111
  2. Octal : $5557_8$:
    • To obtain this, group the binary digits into groups of 3 bits from right to left and convert them to its corresponding octal representation.
    • 101 101 101 111 : 5557$_8$
  3. Decimal : 2927
  4. Hex: 0xB6F
    • To obtain this, group the binary into groups of 4 bits from right to left as well, and convert each group to its corresponding hex representation.
    • 1011 0110 1111 : 0xB6F

Example 2:

  1. Binary : 111 110 101
  2. Octal : $765_8$
  3. Decimal : 501
  4. Hex:
    • Pad the higher bits of the binary so that the total number of bits is the closest divisible by 4. In this case, we expand from 9 bits to 12 bits by adding three 0s at the higher bits. Notice that this does not change the numerical value of the binary string.
    • 111 110 101 is equivalent to 0001 1111 0101, hence 0x1F5

2’s Complement

2’s Complement is the way most computers or electronic machines choose to represent signed integers. Given a string of bits, we can compute its negative representation using 2’s Complement.

Firstly, most computers chooses to use the most significant bit (MSB) as the indicator of whether a particular integer is positive or negative.

You can’t tell whether a device supports signed or unsigned bits by staring at its output bits. This information need to be given to you beforehand, i.e: given when you bought the machine, or given to you in problem sets or quiz.

For example:

  • 00101 is a positive number: $2^2 + 2^0 = 5$
  • 11011 is a negative number: $-2^4 + 2^3 +2^1+ 2^0 = -16 + 8 + 2 + 1 = -5$

To compute the 2’s Complement representation of $5$ and represent a negative version of it in a computer, we need to apply the following mathematical operation to the original bits:

  • Step 1: inverse all 0s into 1s and vice versa on the original binary number
  • Step 2: add 1 to the number in step 1

Example: 0 0 1 1 = 3 $\rightarrow$ we want to turn this into -3, so we do the steps below: Step 1: 1 1 0 0 (inversed)
Step 2: 1 1 0 0 + 0 0 0 1 = 1 1 0 1 (add 1) The value of the result of step 2 above is : $-2^3 + 2^2 + 2^0 = -3$.

The 2’s Complement is an operation that can be applied to either numbers: the positive or the negative, and it will yield its counterpart.

Bonus: Decimal Encoding

How to encode decimal in binary? We extend our prior knowledge. Suppose we have signed binary number:

    1 0 0 1 . 0 0 1 1

The above means $-1 \times 2^3 + 1 \times 2^0 + 1 \times 2^{-3} + 1 \times 2^{-4}$.

Encoding

Encoding is the process of assigning representations to information. Strings of bits can mean some value of integers, but we can also assign a fixed repesentation to them.

For example, given four choices A, B, C, and D, we can assign two bits each to encode each choice: 00, 01, 10, 11 if they are equally probable.

More precisely, it is called the fixed length encoding, that is used in practice when all choices $x_i, i=1,…N$ are equally probable.

There also exist variable length encoding but we will not learn that in this course.

Example of encoding is character encoding so that the string of bits can be displayed to us properly:

  • Number Encoding : 4-bits to represent each number 1 to 10:
  • 7-bit ASCII encoding for english characters
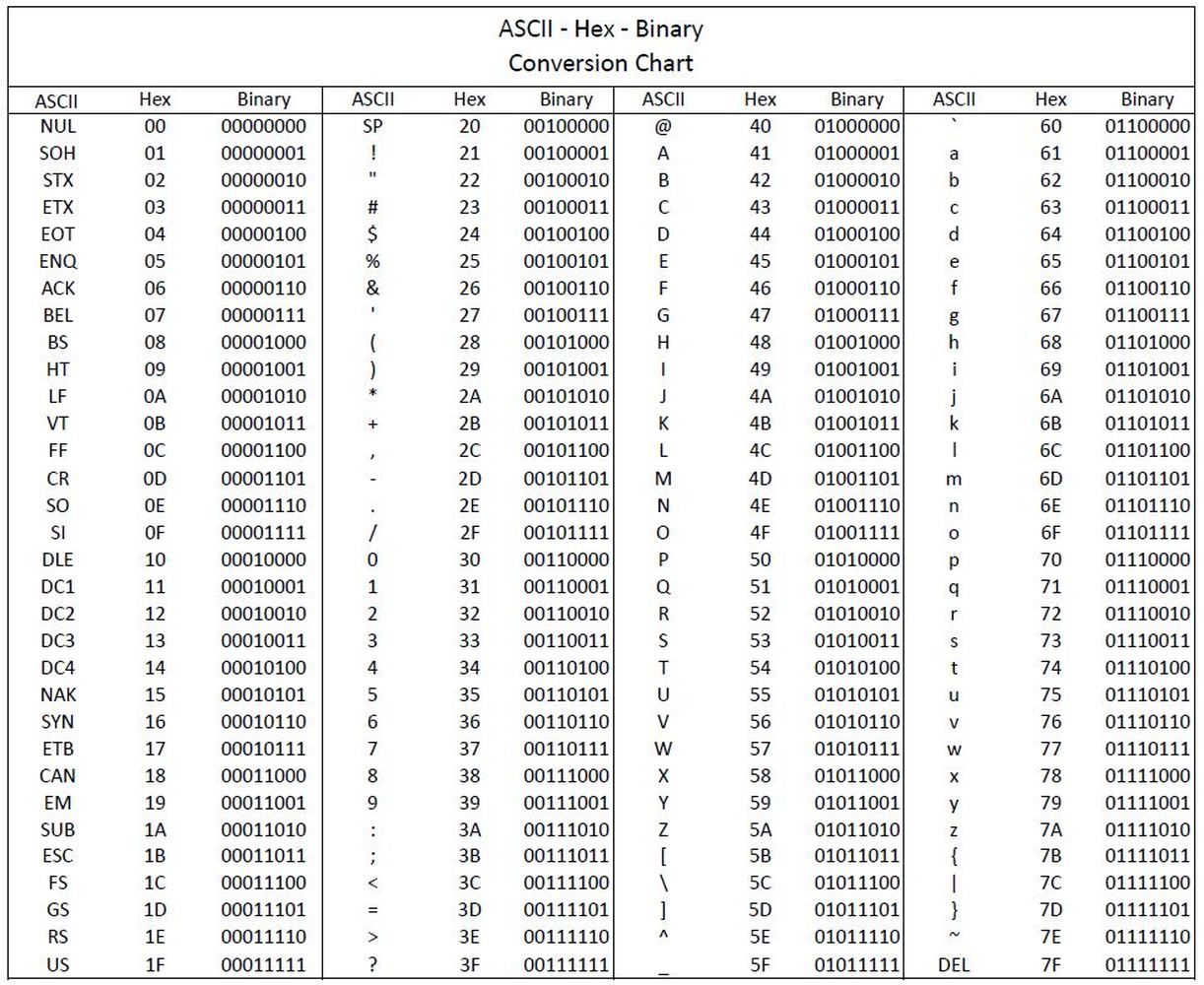
  • 16-bit Unicode (UTF-16) encoding: for other language alphabets that are fixed, e.g: Russian, Korean

We can create electronic devices that are able to map (decode) a given encoded information, perform computations based on the received information, and encode back the output so that the results can be interpreted by us (users) or other devices.

Information and uncertainty

The amount of information held by an event is inversely proportional to the probability $p$ of that event happening,

\[\begin{aligned} \text{Information } \propto \text{ Uncertainty} \propto \text{ }\frac{1}{p}.\end{aligned}\]

Equivalently, it is proportional to the uncertainty of that event happening.

More precisely, to the logarithm of the uncertainty of the event happening. However since log is an increasing function, the sense of proportionality remains the same.

In laymen terms: If an event is bound to happen, then the fact that the event happens does not give any kind of information

For discrete events $(x_1, x_2, … , x_N)$ with probability of occurence of $(p_1, p_2, …, p_N)$, the basic measure of information for all of these events is the bit.

The number of bits is needed to reveal that a random variable is $x_i$ is:

\[\begin{aligned} I(X) = \log_2 \frac{1}{p_i} \text{ bits},\end{aligned}\]

where $I(X)$ is the amount of information received in bits learning that the choice was $x_i$.

Example: Let $N = 8$, and all 8 events are equally probable. The number of bits needed to encode all 8 events are:

\[\begin{aligned} I(X) &= \log_2 \frac{1}{1/8} = 3 \text{ bits}. \end{aligned}\]

We need to receive 3 bits of information to learn that one event $x_i$ out of the 8 events happens. In this case, it can be 000, 001, 010, 011, 100, 101, 110, and 111.

With $N$ equally probable choices, if it is narrowed down to $M$ choices (where $N>M$), then we can say that we are given

\[\begin{aligned} I_{N\rightarrow M}(X) = \log_2 \left( \frac{N}{M} \right) \text{ bits of information}\end{aligned}\]

Following from the example above, if our pool of possible events are narrowed down to 3 from 8, then intuitively we only need 2 bits (instead of 3) to encode 3 different events, e.g: 00, 01, and 10. Therefore we know we are given at least 1 bit of information.

With the formula above, N=8, M=3, therefore:

\[\begin{aligned} I_{8\rightarrow 3}(X) = \log_2 \left( \frac{8}{3} \right) = 1.42 \text{ bits of information}\end{aligned}\]

Summary

This chapter quickly summarises how we can represent integers using different number systems, especially the binary number system that is especially useful for our computers since they can only store information in terms electrical voltages (representing simply strings of 1s and 0s).

Given $X$ bits,

  1. We can encode $2^X$ choices, or random variables

    Equivalently, given $Y$ choices, we need to use at least $\log_2(Y)$ bits to encode them, rounded up to the nearest integer (since we cannot technically subdivide “bits” in real life.

  2. If it is unsigned, we can represent the number ranged from 0 to $2^X-1$

  3. If it is signed, we can represent the number ranged from $-2^{X-1}$ to $2^{X-1}-1$

The prior knowledge of whether a device support signed or unsigned bits must be given to you.

Post Conclusion

Finally, you might be wondering why are we counting the number of bits required to encode some amount of information, and why do we bother with encoding information in terms of bits at all. As said in the introduction, the goal of this course is to learn how to build a general-purpose digital device (computers).

  • We begin the first half of our learning journey by trying to create a digital device (not for general purpose yet) that’s for a specific purpose, for example:
    • a simple device that can perform 1-bit addition (Mini Hardware Project),
    • a simple device that can perform basic logic computation: addition, subtraction, bitshift, boolean operation (SW Lab 3: ALU),
    • a simple electronic game device that can take input from players, compute it, and determine the winner (1D Project)

  • Regardless of the specific purpose, we need a way to implement the logic (“addition” logic for example) for this machine. If we were to explain the workings of an adder to you, it will be pretty easy because we use the English language to communicate all the necessary information for you to understand how it works.
    • Explaining this logic to a machine isn’t quite as easy because they don’t understand English – they only can comprehend “low” and “high” voltages. Therefore we have to move the domain of which we convey information in terms of binary digits (bits), and get used to encoding logic (information) in this domain.

  • Once we are comfortable with conveying logic (information) in terms of bits, then we have to start finding components that can manipulate voltages, and this component is called a transistor – which you will learn pretty soon.

    The problem sets are created so that you’re comfortable with bit manipulation and communicating (with your future machine) in that domain.

    Note that transistor is not the first tool created to manipulate voltages: triode vacuum tubes and electro-mechanical relays were used in pre-1950s. Before electricity was discovered, people used mechanical gears and punch cards to encode digital data.

    Digital data is the discrete, discontinuous representation of information or works.

  • If you Google “triode vacuum tubes”, and “electro-mechanical relays” – or even the “early transistors”, you’d realise that they have quite a large size and they are definitely not cheap. You can find some information here for context, but on average in the past it costs about $8 each. They cost about a billion times more than they are now, so your computers that have billions of transistors might cost you a few billion $ in the past (not to mention that it would’ve been enormous in size too).

    It might be unimaginable how big and expensive computers were at first because we are so used to having portable computers – consisted of billions of cheap and extremely small transistors (5-7nm) and pretty much “unlimited” storage unit (we can always buy external drive, cloud storage, extend our RAM or simply buy computers with terabytes of disk size). But in the past – life wasn’t quite as easy.

  • With this in mind, it makes sense that if someone (in the past) were to make a digital device from scratch, he or she has to be mindful with the size and cost of the device, and therefore has to be mindful with counting (and probably minimising) how many bits are needed to contain all information and logic necessary for the intended device to work.

  • But having a digital device that can do only that specific job: just addition, just that game logic, or just playing a VCD (VCD player) is not enough. We do not want to:
    • Have so many devices to carry.
    • Spend so much money to buy 1 device for each task
    • It will be ridiculous now to imagine if we need 1 separate, physical device for everything: 1 device to browse, 1 device for each video game, 1 device for chatting with a particular person, 1 device for computing addition, 1 device for computing division.. you get the idea.

  • Therefore towards the middle of the term, we will learn how to create a better digital device: a programmable one that is suitable to be used for a plethora of purposes without any hardware changes – and can manipulate, store, and produce digital data.
    • We will consider all things necessary to create this programmable device that can tend to various general purposes (not just limited purposes) – meaning to create a device that can emulate the behavior of many other devices (given a description of how that other devices work: software), so that we simply just need to get this ONE device to perform many tasks and computations. This device is none other than our computers.

      “Computers” include any device: your laptops, desktops, and smartphones, etc for which you can install and run various kinds of software.